| |

Fracciones
|

Para poder
tomar los exámenes
de este tema
debes estar
registrado, si
no lo estás,
Registrate
aquí
Entrar a exámenes
de:
Contenido Revisado 
|
|
|
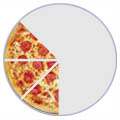
Una fracción es una parte de un total
Corta una
pizza en trozos, y tendrás fracciones:
 |
 |
 |
|
1/2
|
1/4
|
3/8
|
|
(Una mitad)
|
(Un
cuarto)
|
(Tres octavos)
|
|
|
|
|
|
El número
de arriba te dice cuántas porciones
tienes y el de abajo te dice en
cuántos trozos se ha cortado la
pizza. |
Numerador / Denominador
Al número de
arriba lo llamamos Numerador, es el
número de partes que tienes.
Al de abajo lo llamamos Denominador, es
el número de partes en que se ha dividido el
total.
¡Sólo tienes
que recordar esos nombres! (Si los confundes,
recuerda que denominador es con "D" de dividir)
Fracciones
equivalentes
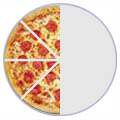
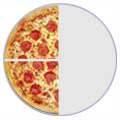
Algnas fracciones
parecen diferentes pero en realidad son la misma,
por ejemplo:
|
|
4/8
|
= |
2/4
|
= |
1/2
|
|
| |
(Cuatro
octavos) |
|
(Dos
cuartos) |
|
(Una mitad) |
|
|
|
 |
|
 |
|
 |
|
Normalmente lo
mejor es dar la respuesta usando la fracción más
simple (1/2
en este caso). Eso se llama Simplificar
o Reducir la fracción.
Sumar
fracciones
Puedes sumar
fracciones fácilmente si el número de abajo (el
denominador) es el mismo:
|
|
1/4
|
+ |
1/4
|
= |
2/4
|
= |
1/2
|
|
|
|
(Un cuarto) |
|
(Un cuarto) |
|
(Dos
cuartos) |
|
(Una mitad) |
|
|
|
 |
|
 |
|
 |
|
 |
|
Otro ejemplo:
Sumar fracciones con
denominadores diferentes
¿Y si los
denominadores no son iguales? Como en este
ejemplo:
Deberías hacer que los denominadores fueran
iguales de alguna manera. En este caso es
fácil, porque sabemos que
1/4
es lo mismo que 2/8
:
En ese ejemplo
fue fácil hacer que los denominadores fueran el
mismo, pero puede ser más difícil... visita las
páginas de los métodos de |
|
Fracciones Equivalentes
Las Fracciones Equivalentes
tienen el mismo valor, aunque parezcan
diferentes.
Estas fracciones
son en realidad lo mismo:
¿Por qué son lo mismo? Porque cuando
multiplicas o divide a la vez arriba y
abajo por el mismo número, la fracción mantiene
su valor. La regla a recordar es:
¡Lo que haces a la
parte de arriba de la fracción
también lo tienes que hacer a la parte de abajo!
Por eso, estas
fracciones son en realidad la misma:
|
|
× 2 |
|
× 2 |
|
|
|
|
1 |
= |
2 |
= |
4 |
| |
|
|
|
2 |
4 |
8 |
|
|
| |
× 2 |
|
× 2 |
|
Y en un dibujo
se ve así:
Aquí hay más
fracciones equivalentes, esta vez dividiendo:
|
|
÷ 3 |
|
÷ 6 |
|

 |
|
18 |
= |
6 |
= |
1 |
| |
|
|
|
36 |
12 |
2 |

 |
| |
÷ 3 |
|
÷ 6 |
|
Si seguimos dividiendo hasta que no podamos más,
habremos simplificado la fracción (la
hemos hecho la más simple posible).
Importante:
- Las partes
de arriba y abajo de la fracción siempre
deben ser números enteros.
- Las
operaciones que podemos hacer son
multiplicar y dividir (siempre las dos
partes a la vez). Si sumamos o restamos un
número arriba y abajo, no tendremos
una fracción equivalente.
- El número
que elijas para dividir las dos partes no
debe dejar ningún resto en las divisiones.
VER
 una explicación hablada
una explicación hablada

|
|
Sumar fracciones
Hay tres
simples pasos para sumar fracciones:
Paso 1:
asegúrate de que los números de abajo (los
denominadores) son
iguales
Paso 2: suma
los números de arriba (los
numeradores). Pon la respuesta sobre el
denominador del paso 1
Paso 3:
simplifica la fracción (si hace falta)
Ejemplo 1:
Paso 1.
Los números de abajo son los mismos. Ve
directamente al paso 2.
Paso 2.
Suma los números de arriba y pon la respuesta
sobre el denominador:
|
1 |
+ |
1 |
= |
1 + 1 |
= |
2 |
| |
|
|
|
|
4 |
4 |
4 |
4 |
Paso 3. Simplifica
la fracción:
(Si no
estás seguro de cómo se hace el último paso
ve arriba para que leas de las Fracciones
equivalentes)
Ejemplo 2:
Paso 1: los
números de abajo son diferentes. Así
que necesitamos hacerlos iguales.
Podemos
multiplicar arriba y abajo de
1/3
por 2 así:
y ahora los
números de abajo (los denominadores) son
iguales, nuestro problema queda así:
Paso 2: suma los
números de arriba y ponlos sobre el mismo
denominador:
|
2 |
+ |
1 |
= |
2 + 1 |
= |
3 |
| |
|
|
|
|
6 |
6 |
6 |
6 |
Paso 3: simplifica
la fracción:
Hacer los
denominadores iguales
En el
ejemplo anterior fue fácil hacer que los
denominadores fueran iguales, pero puede ser
más difícil... así que necesitarás usar el
|
|
Mínimo denominador
común
... es el Mínimo
común múltiplo de los denominadores...
Primero, vamos a recordar lo
que es el denominador:
Fracciones
Una fracción (como
3/4) tiene dos
números:
Al número de arriba lo llamamos
Numerador, es el número de partes que tienes.
Al de abajo lo llamamos Denominador, es el número de
partes en que se ha dividido el total.
Fracciones con denominadores
diferentes
A veces tienes dos (o más)
fracciones con denominadores diferentes - a lo mejor quieres
sumarlas o restarlas - pero necesitas tener los mismos
denominadores antes de poder hacerlo:
Ejemplo: ¿Cuánto es
3/8 +
5/12 ?
Vamos a probar a hacer que los
denominadores sean el mismo... si multiplicas 8 × 3 sale
24, y su multiplicas 12 × 2 también sale 24. Así que
probemos con eso (importante: lo que hagas abajo, debes
hacerlo también arriba):
Ahora podemos sumar:
9/24 +
10/24 =
19/24.
Cómo poner el mismo
denominador
El truco es calcular el
Mínimo común múltiplo de los denominadores.
En el ejemplo de antes, el mínimo común múltiplo de 8 y 12 era
24. Y por eso el mínimo común denominador de
3/8 y
5/12 es
24
Así que, aquí están los pasos:
 |
- Calcula el
mínimo común múltiplo de los denominadores (se
le llama el mínimo común denominador).
- Cambia cada
fracción (usando fracciones equivalentes) para que
los denominadores sean iguales al mínimo común
denominador.
- ¡Ya puedes hacer
lo que quieras con las fracciones (sumar, restar)!
|
| |
Ejemplo: ¿Cuánto es
1/6 +
7/15 ?
El mínimo común mútiplo
de 6 y 15 es 30 (¡intenta calcularlo tú mismo!).
Así que vamos a multiplicar para que cada denominador
sea igual a 30:
|
Mínimo común
múltiplo
El número más
pequeño (no cero) que es múltiplo de dos o más números.
El nombre de mínimo común
múltiplo está hecho de las partes mínimo, común
y múltiplo:
¿Qué es un "múltiplo"?
Los múltiplos de un número son
lo que tienes cuando lo multiplicas por otros números (si
lo multiplicas por 1,2,3,4,5, etc.) como en las tablas de
multiplicar.
Aquí tienes ejemplos:
| Los múltiplos de
3 son 3, 6, 9, 12, 15, 18, 21, etc... |
| Los múltiplos de
12 son 12, 24, 36, 48, 60, 72, etc... |
¿Qué es un "múltiplo común"?
Si tienes dos (o más) números,
y miras entre sus múltiplos y encuentras el mismo valor en las
dos listas, esos son los múltiplos comunes a los
dos números.
Por ejemplo, si escribes los múltiplos de dos números diferentes
(digamos 4 y 5) los múltiplos comunes son los que están
en las dos listas:
| Los
múltiplos de 4 son 4,8,12,16,20,24,28,32,36,40,44,... |
| Los
múltiplos de 5 son 5,10,15,20,25,30,35,40,45,50,... |
| |
| ¿Ves que
20 y 40 aparecen en las dos listas? Entonces, los
múltiplos comunes de 4 y 5 son: 20, 40 (y 60, 80,
etc. también) |
¿Qué es el "mínimo común
múltiplo"?
Es simplemente el más
pequeño de los múltiplos comunes. En el ejemplo anterior, el
menor de los múltiplos comunes es 20, así que el mínimo
común múltiplo de 4 y 5 es 20.
Calcular el mínimo común
múltiplo
En realidad es muy fácil de
hacer. Sólo escribe los múltiplos de los números hasta que
encuentres uno que coincida.
Ejemplo 1: encuentra el mínimo
común múltiplo de 3 y 5:
| Los múltiplos de 3
son 3, 6, 9, 15, ..., y los múltiplos de 5
son 5, 10, 15, 20, ..., así: |
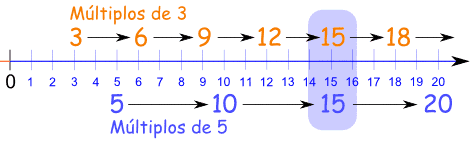 |
| Como puedes
ver en esta línea de números, el primer múltiplo que
coincide es el 15.
Respuesta: 15 |
Y puedes calcular el mínimo
común múltiplo de 3 (o más) números.
Ejemplo 2: calcula el mínimo
común múltiplo de 4, 6 y 8
Los múltiplos de 4
son: 4, 8, 12, 16, 20, 24, 28, 32, 36, ...
Los múltiplos de 6 son: 6, 12, 18, 24, 30, 36,
...
Los múltiplos de 8 son: 8, 16, 24, 32, 40, ....
Entonces 24 es el mínimo
común múltiplo de (¡no podemos encontrar uno más
pequeño!) |
Pista: puedes hacer listas
más pequeñas de los números más grandes. |
|