Integrales elípticas
Fecha de primera versión: 16-04-02
Fecha de última actualización:
19/04/2010
![]()
![]()
Reciben este nombre porque aparecen al calcular la longitud de las elipses.
La integral elíptica general tiene la forma ![]()
Legendre, que fue el primero que las estudió, clasificó las integrales elípticas en tres tipos:
Integrales elípticas de primera especie: ![]()
Integrales elípticas de segunda especie: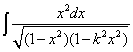
Integrales elípticas de tercera especie:![]()
Como x necesariamente tiene que ser menor que 1, pues de lo contrario la raíz se haría negativa, podemos hacer el cambio x = sen f nos queda:
Integrales elípticas de primera especie: 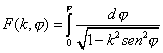
Integrales elípticas de segunda especie: 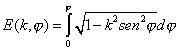
Integrales elípticas de tercera especie: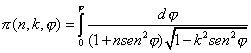
Abel y Jacobi, también estudiaron las integrales elípticas.
Las funciones elípticas son una generalización de las funciones circulares e hiperbólicas. Cuando k = 0 la integral elíptica se convierte en:
![]()
Cuando k = 1
![]()