M A T E M Á T I C A S

Aprendamos a Medir

Enseñar a medir implica acompañar a los chicos mientras miden y miden. La idea es aprender a medir. Digo esto porque cuando se habla de “medida” en la clase de matemática, generalmente se trata de cálculos escritos con medidas ya calculadas. Lo que propongo en cambio, es enseñar a medir.

El concepto matemático de medir es bastante complejo. Si bien en 1° no se desarrollan estos conceptos, el docente tiene que tener claro para qué está preparando a sus alumnos. Por eso empezaremos con una repasadita.

Gran variedad

En el mundo físico hay una gran variedad de cosas a medir. Y cada objeto tiene, a su vez, varios aspectos a medir.

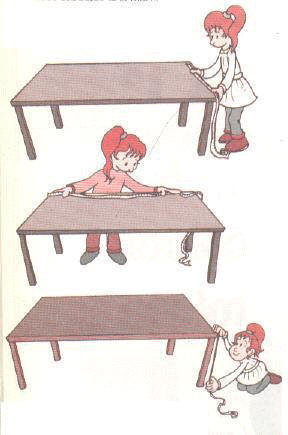
El largo, el ancho y el alto son longitudes.

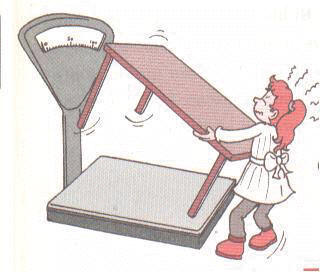
Esta chica está midiendo el peso de la mesa con una balanza.

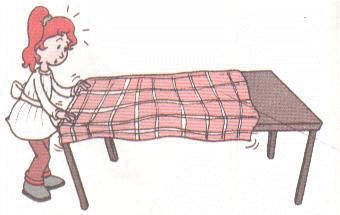
La mesa tiene una superficie mayor que la del mantel.

Magnitudes

El peso, la longitud, la superficie, son magnitudes y también lo son el tiempo, la capacidad, el volumen.

Nueve pulgadas, el largo de un auto, el ancho de la bañera, la altura de un chico, son cantidades de la magnitud longitud. De la misma forma que el lugar que ocupa una montaña, un metro cúbico y el espacio que ocupa nuestro cuerpo, son cantidades de volumen.

Cómo se mide una cantidad

Para medir una cantidad de una magnitud hay que elegir una unidad de medida. Esa unidad de medida tiene que cumplir el requisito de pertenecer a la misma magnitud que lo que se quiere medir.

Para medir la longitud de una soga, la unidad de medida debe ser una cantidad de longitud. En el ejemplo de la figura se tomó como unidad de longitud el largo del bastón.

La soga mide 10 pies, con la regla (o bastón) de tres pies o losetas de 12 pulgadas como unidad de medida. Al medir se hace una operación matemática: la división.

Para medir una cantidad de capacidad, la unidad de medida es otra capacidad y para medir se calcula una división.

De la misma forma, para medir una superficie la unidad de medida es otra superficie y se calcula una división.

Para medir un peso la unidad de medida es otro peso. Calcular la medida es dividir.

La cuestión de medir, como involucra la división tiene toda la complejidad  del concepto de división, de la cuenta de dividir, de las fracciones y los decimales.

Expertos en medidas

¿Quién no ha ideo a la carniceria y le ha pedido al carnicero 5 libras de Bistec  y lo ha visto pesar la carne y casi por sorpresa vemos que los 10 pedazos que puso en la balanza pesaban justamente las 5 libras. La práctica y costumbre del carnicero le ayuda a determinar cuantos pedazos pueden pesar las libras de carne que le soliciten.

Este conocimiento que han logrado algunas personas sobre las medidas, fruto de la práctica, del ensayo y el error, es la que tiene que inspirar la enseñanza de la medida en la escuela. Una vez conseguida, ya se podrá teorizar con cosas abstractas como los algoritmos y cosas por el estilo. Es por eso que la tarea escolar referida a la medida deberá basarse en mucha práctica de comparación de cantidades y, para eso, acá van algunas ideas.

Paso a paso

A esta altura vale una aclaración importante. Todo el trabajo con las unidades convencionales de medida, los números decimales, etcétera, es muy posterior a esa práctica a la que hago referencia más arriba. Para probar eso basta recordar los desvelos que persiguen a maestros y alumnos de segundo ciclo cuando se pretende ventilar en clase problemas de medidas y se recurre a la famosa tablita para reducir y a otos algoritmos para calcular. Así como los chicos de 1° no pueden comprender el sistema de numeración si no tienen mucha experiencia de contar, de la misma forma, saber calcular con medidas requiere el paso previo de tener experiencia concreta de magnitudes y cantidades.

Medir en la cocina

En la cocina siempre hay material para el cálculo y la matemática. El asunto de las medidas es, a no dudarlo, un tema de cocina. Vasitos medidores, balanzas y otros instrumentos de medición se encuentran a disposición en la cocina; los libros de cocina están hechos a base de medidas, pero lo que quiero destacar acá son las actividades en las que los chicos manipulan cantidades, las comparan y sacan conclusiones a aproximadas de sus medidas.

¨           Vasos, jarras, tazas, cacerolas, todos estos recipientes son apropiados para medir la capacidad. Pasando agua de un recipiente a otro, los chicos irán construyendo la idea de capacidad de los recipientes y que esas capacidades se pueden comparar, ordenar de mayor a menor, se pueden medir. No hay que olvidar otros recipientes en la cocina menos usados a la hora de pasar líquidos que, justamente por eso, ayudan a construir la idea de capacidad de los recipientes y sus medidas.

• ¿Cuántas cucharadas de café se necesitan para llenar una de sopa?

• ¿Cuántos platos llanos llenos hasta el borde con agua son necesarios para llenar un plato hondo?

• ¿Cuál contiene más sopa, un plato hondo un tazón?

• La capacidad de los recipientes se puede comprobar con agua, leche o líquidos de uso doméstico y también granos como las habichuelas o fideos.

• Repartir entre los chicos varios frascos de cocina transparentes. La maestra(o) muestra otro frasco igual pero con lentejas (ni muy lleno ni muy vacío) que será usado para comparar. Se pide a los chicos que pongan agua en sus recipientes, una cantidad menor que la del modelo con lentejas (o mayor, o igual).

• Una vez cumplida la consigna se pueden comparar los frascos, ordenarlos de menor a mayor, de mayor a menor o juntar los que tienen igual cantidad.

• Se puede pedir que llenen frascos hasta la mitad y luego comprueben que, efectivamente, se necesitan dos mitades para completar un frasco.

• Más difícil: conseguir en su frasco una cantidad mitad de la cantidad que tiene el frasco del docente.

• Si tuvieras una mochila mágica, ¿qué guardarías dentro de ella? Haste un dibujo. Después fijate cuántas naranjas entran en tu mochila, cuántas mandarinas y cuántos melones.

• Con un frasco de antibiótico (vacío) y su tapa para medir llenar el frasco con agua y calcular cuántas dosis contiene el frasco.

• Hacer una fila con cucharitas para comparar el largo con el de la mesa. Tomar el largo de una mesa para compararlo con el del salón, el patio, la vereda o… vaya a saber qué.

• Hacer un acopio de fruta, llenar bolsas iguales transparentes, ver cuántas caben en cada una: bananas, manzanas, frutillas, pomelos, etcétera. Si el volumen de la fruta es más grande que el que puede contener la bolsa, por ejemplo, una sandía, los chicos podrán comprobar que “en la bolsa cabe menos que una sandía”, concepto que más adelante dará lugar a las medidas menores que la unidad.

• Con balanza de dos platillos se puede calcular cuántos panes entran en un kilo, cuántas naranjas, manzanas, etcétera.

• El rollo de cocina es un material excelente para medir longitudes y también superficies. ¿Qué es más largo, el rollo de cocina desenrollado, por supuesto, o la vereda de la escuela? ¿Cuántas servilletas del rollo de cocina se necesitan para cubrir el escritorio de la maestra?

Medir con el cuerpo

Medir con le cuerpo es de suma importancia para que los chicos construyan los conceptos matemáticos desde lo concreto. Basta pensar que la humanidad, en tiempos remotos, comenzó midiendo longitudes con partes del cuerpo: la mano (palma), el brazo, etcétera.

• Marcar en la pared registrando la altura de los chicos, comparar con las alturas en una foto, renovar las marcas a lo largo del año escolar, todo eso es trabajar con la medida de la altura del cuerpo.

• ¿Y por qué no un registro del ancho del cuerpo de los chicos?

• La fila, de mayor a menor o de menor a mayor, son ordenamientos por altura y por eso involucran el concepto de medida de longitud.

• Calcular cuántos chicos en fila se necesitan para cubrir el largo del patio, es medir una longitud pero también se puede medir ese largo con los chicos puestos tomados de la mano, acostados haciendo en el piso una fila, uno a continuación de otro. Cambiando la disposición de los chicos para medie el patio, se lleva la atención sobre el problema de cambiar la unidad de medida para medir una misma cantidad y la relación que existe entre la medida y la unidad.

• Cuanto mayor es la unidad, la medida es menor al medir una misma cantidad. Con el cuerpo de los chicos se puede medir superficies. ¿Cuántos chicos acostados llenan una colchoneta?, ¿sentados?, ¿parados,?, ¿en cuclillas?

• El cuerpo ocupa un volumen. ¿Cuántos chicos caben en el interior del armario?

Números a la fuerza

Con un acopio de latas de conserva (tomates, habichuelas, etcétera), proponer un concurso a ver quién sostiene más.

¨           El sube y baja constituye una verdadera balanza casera que permite comparar los pesos que sostiene en sus puntas. Se puede hacer un concurso en el que cada chico y chica, subida al sube y baja, sostiene pesos colocados en la otra punta.

Medir en el patio

• Medir longitudes en un caminito de hormigas. ¿Cuántas hormigas cubren un camino de medio metro de largo?

• Cajones para amontonar. ¿Cuántos cajones se necesitan amontonar  para alcanzar a  la ventana del baño?

• En el arenero, la capacidad de los recipientes se puede medir pasando arena.

• Calcular a ojo medidas de tierra y agua para hacer barro.

• Medir longitudes con hilos y sogas.

• Medir tiempos con una fila de hormigas. ¿Cuántas hormigas pasan  junto a una plantita mientras una de las nenas da una vuelta al patio?

• En cualquier competencia en la que se mide el tiempo con un cronómetro es una actividad con medidas.

• Tarda más, tarda menos, tarda tanto como, son formas de medir el tiempo.

Actividad

Para terminar, llevemos el hilo de la reflexión hacia la naturaleza de los números que se usan para medir. Si bien la Matemática tiene teorías precisas sobre la medida y los números reales dan un marco a esas conclusiones, en 1° habrá que tener en cuenta que los chicos miden con números naturales, 0, 1, 2, 3, etcétera, pero que hay que dejar la puerta abierta para futuros conocimientos involucrando el concepto de partes de un entero.

WWW.PROYECTOSALONHOGAR.COM