|
![]()
GEOMETRíA
Rectas Paralelas y Secantes
|
Aunque se le conoce más por su obra
"Elementos", donde expone brillantemente la Matemática que hasta
aquel momento habían desarrollado los griegos, escribió sobre
diversos temas, como música y óptica. También escribió una obra
titulada "Sofismas", cuyo fin era ejercitar la inteligencia.
Cuenta la historia que el rey Ptolomeo preguntó a Euclides, al constatar lo voluminosa que era su obra "Elementos", si no había un camino más corto para estudiar y dominar la Geometría. Euclides le respondió: "En Geometría no existe un camino especial para los reyes". |
||||||
|
|
||||||
|
||||||
|
Rectas Paralelas y Secantes.
|
||||||
Así puede suceder con
la Geometría. Estudiarla equivale a conocer los objetos de los cuales se
ocupa (rectas, puntos, ángulos, circunferencias, etc.) y a descubrir
poco a poco las reglas del juego que explican cómo se "comportan" esos
objetos.
Nuevas reglas del juego van apareciendo a medida que se domina un nivel
del juego y se dispone el jugador a conocer etapas más avanzadas del
mismo. Por eso, se trata de un juego
que nunca aburre porque siempre habrá nuevas etapas por descubrir, y
nuevos retos que enfrentar.
Los retos consisten en la resolución de problemas geométricos, tomando en cuenta todo lo que se sabe acerca de los objetos que forman parte del problema.
Para comenzar con los objetos más simples de la Geometría: rectas y puntos, puede iniciarse el estudio de estos objetos considerando algunos hechos básicos:
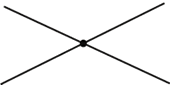 |
-
en este caso, se dice que son paralelas.
b)Las dos rectas no tienen ningún punto en común, aunque se prolonguen indefinidamente en ambas direcciones
 |
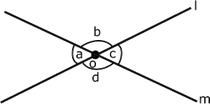 |
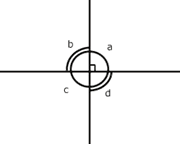
Se observa en la figura de la izquierda que hay cuatro
ángulos con vértice en el punto
![]() .
.
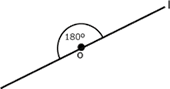
Es importante recordar lo que es un ángulo llano: es el
ángulo formado por dos rayos o semirrectas que pertenecen a una misma
recta, y mide
![]() .
.
 |
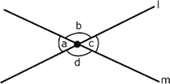 |
Como se ve en la figura de
la izquierda, ![]() y
y ![]() .
.
Simplemente porque
![]() y
y
![]() son rectas. En este caso, se dice que
son rectas. En este caso, se dice que
![]() y
y
![]() son adyacentes, como también lo son
son adyacentes, como también lo son
![]() y
y
![]() .
.
Ahora se puede presentar la primera oportunidad de enfrentar un reto de
la Geometría, asociado a las rectas secantes y los ángulos que forman.
¿Será cierto que
![]() y que
y que
![]() ? Si se quiere "jugar" correctamente el juego de la Geometría, no basta
con responder "sí" o "no". Hay que explicar por qué.
? Si se quiere "jugar" correctamente el juego de la Geometría, no basta
con responder "sí" o "no". Hay que explicar por qué.
Tomando en cuenta la información anterior:
-
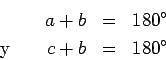
- se tiene que
-
por lo tanto
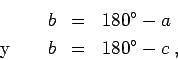
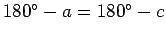 , y esto quiere decir que
, y esto quiere decir que
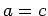 .
.
Hemos concluido que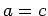 .
.
-
|
Ahora demostremos que b
= d :
Sabemos que d+a = 180 grados y b + a = 180 grados porque m y l so rectas. Por lo tanto a = 180 grados - d y a = 180 grados - b es decir, 180 grados - b = 180 grados - d y así queda demostrado que b = d . |
Los ángulos
Se acaba de deducir una "regla" importante del juego con rectas secantes en un plano: los ángulos opuestos por el vértice son congruentes, es decir, tienen la misma medida.
Si un ángulo formado entre dos rectas secantes es recto (es decir, mide
A continuación mostraremos que si un ángulo entre dos rectas secantes es recto, también lo son los otros 3 ángulos que se forman:
|
Observa la figura:
Sabemos que a = c
por ser opuestos por el vértice. Como a =
90 grados, c = 90 grados,
c+d = 180 grados, por ser c y
d adyacentes. como d = b por ser opuestos por el vértice, resulta que b = 90 grados. |
Ahora se puede avanzar un poco y considerar las posiciones relativas de tres rectas en el plano.
Hay cuatro posibilidades:
1) Las tres rectas son paralelas:
|
|
2) Dos rectas son paralelas y una es secante:
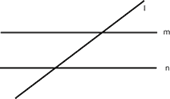 |
 |
4) Las tres rectas se cortan en un solo punto:
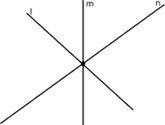 |
- Las opciones 2 y 3 generan situaciones llenas de propiedades nuevas e interesantes.
Los triángulos, que surgen de las figuras del tipo 3) se estudiarán más adelante.
En lo que sigue, se explorarán las propiedades de los ángulos que se generan en las figuras del tipo 2).
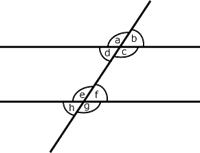
Para hablar con precisión, hay que comenzar por darle nombres a los ángulos que se forman:
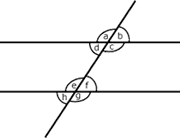 |
Los ángulos
![]() y
y
![]() se dice que son correspondientes.
se dice que son correspondientes.
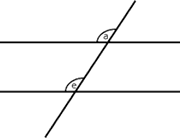 |
También lo son
![]() y
y
![]() ,
,
![]() y
y
![]() ,
,
![]() y
y
![]() .
.
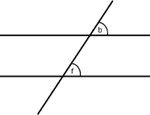 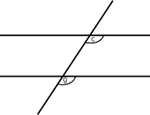 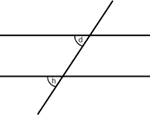 |
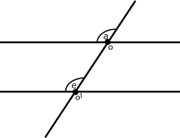 |
Una propiedad importante de los ángulos que se forman entre dos rectas paralelas, es la siguiente:
Los ángulos correspondientes son congruentes.
Si se hiciera una traslación del punto
![]() al punto
al punto
![]() en el siguiente dibujo, como las rectas horizontales son paralelas,
se ve que el ángulo
en el siguiente dibujo, como las rectas horizontales son paralelas,
se ve que el ángulo
![]() coincidiría con el ángulo
coincidiría con el ángulo
![]() .
.
Por otra parte, se sabe que los ángulos opuestos por el vértice son
congruentes, y así, se tiene:
 |
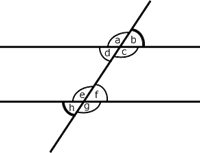 |
Como![]() por ser opuestos por el vértice y
por ser opuestos por el vértice y
![]() por ser correspondientes, se tiene que
por ser correspondientes, se tiene que
![]() .
.
Los ángulos
![]() y
y
![]() se dice que son alternos externos.
se dice que son alternos externos.
 |
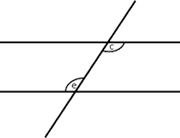 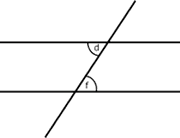 |
|
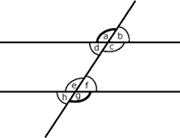
Hay que ver que c = e
y que d = f. Como c = a
por ser opuestos por el vértice, y a = e
por ser ángulos correspondientes, se obtiene que c =
e.
Por otra parte, como d = b por ser opuestos por el vértice y b = f por ser ángulos correspondientes, se obtiene que d = f . |
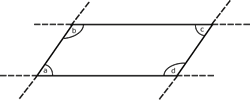
Consideraremos ahora el siguiente pralelogramo:
 |
(los lados son paralelos, dos a dos).
Usando las propiedades estudiadas antes, demostraremos que:
- i) b = d
- ii) a = c
- iii) a + b = 180 grados
- vi) a + b + c + d = 360 grados
|
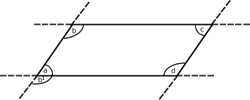
Se prolongan los lados del
paralelogramo como se muestra en la figura:
Se puede ver que las dos
rectas horizontales son paralelas (por tratarse de un
paralelogramo) y los ángulos
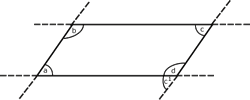
Como Por otra parte, las dos rectas no
horizontales son paralelas, y por lo tanto, entre los
ángulos que ellas forman con la horizontal de abajo, están
Para demostrar las partes ii) y iv), se
observa que los ángulos
Por lo tanto,
|
Ver:
WWW.PROYECTOSALONHOGAR.COM
Bibliografía:
García, V., Villaseñor, R., Waldegg, G.
Matemáticas en contexto - segundo curso.
México: Grupo Editorial Iberoamérica.