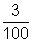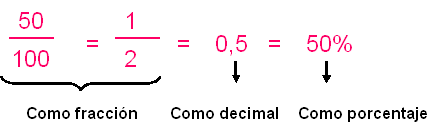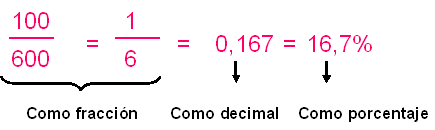| |
|
L a G r a n E n
c i c l o p e d i a I l u s t r a d a d e l
P r o y e c t o S a l ó n H o g a r |
|
|

Razones, porcentajes y
probabilidad

|
Razón
Cuando se establece una comparación entre dos
números, lo que estamos haciendo es sacar una razón, en
otras palabras, una razón, es el cociente entre dos
números.
Cuando se involucran más de dos números o
cantidades, lo que se saca es una proporción, su
definición formal es: "Se denomina proporción a la
igualdad de dos razones".
Al buscar la
razón
entre dos números, pensemos en 42 y
en 36, (que en realidad podrían ser cualquier número),
su razón está dada por el cociente de: 42/36 = 1 entero
1/6
que se lee 42 es a 36, donde el
42
es el
antecedente
y el 36
es el
consecuente.
Nota Importante.-
La diferencia entre una fracción y una una razón
es que, por definición una fracción consta de
números enteros, tanto en el numerador como en
el denominador, mientras que en una razón tanto
lo que sería el numerador, que en realidad es el
antecedente, como el denominador, que en
realidad es el consecuente, pueden ser números
enteros, decimales, fraccionarios
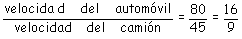
Al comparar las velocidades de un automóvil que
va a
80
km./h
y un camión que va a
45
km./h,
se tiene que:
La velocidad del automóvil es
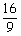 de la del camión.
de la del camión.
Al comparar las velocidades del camión y del
automóvil se tiene que:
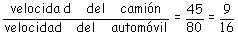
La
velocidad del camión es ,
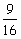 de la
del automóvil. de la
del automóvil.
Se define
como Razón
Equivalente a todas aquellas
comparaciones en donde los resultados son iguales, por
ejemplo: (42-36) y
(76-70) son razones
equivalentes, ya que la razón es 6 en ambos casos. A
razones equivalentes. |
Veánse los siguientes ejemplos de razón:
En un grupo de 32 alumnos 6 reprobaron
español.
Si se presenta como razón queda:
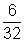 y al simplificar se tiene, y al simplificar se tiene,
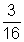 es decir, que reprobaron
español 3 de cada 16 alumnos. es decir, que reprobaron
español 3 de cada 16 alumnos.
Se realizó un concurso de conocimientos en
el que participaron 20 personas; de ellas sólo pasaron a la
etapa final 5, es decir, 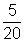 Esta es la representación en forma de razón que simplificada
queda
Esta es la representación en forma de razón que simplificada
queda 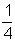 Dicho de otra forma;
1 persona de cada 4 pasó a la final. Dicho de otra forma;
1 persona de cada 4 pasó a la final.
En una fábrica de focos, de cada 100 que
se probaron, se encontró que 3 no encendían. Por lo tanto, la
razón que representa esto es
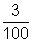
A este tipo de razones que relacionan al
100 con otro número se le conoce como tanto por ciento y
se indica con el símbolo %.
Por otra parte
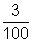 puede expresarse como 0.03
o 3% puede expresarse como 0.03
o 3%
Enseguida, se presenta otro problema de
obtención del tanto por ciento.
En la compra de un producto, descuentan el
10% en pago en efectivo. Si el precio normal del producto es de
$400.00, ¿a cuánto asciende el descuento? Este problema puede
resolverse desglosando el precio en 100, quitando $10 a cada
ciento y sumando todos los descuentos; pero este procedimiento
además de tardado, puede incluir más fácilmente a error, por lo
que se puede sintetizar en la multiplicación del precio por el
tanto por ciento de descuento. Véase:
( $ 400.00) (10%) = (400) (.10) = 40.00
Al resultado que se obtiene se le llama
porcentaje.
Así que el monto del descuento es de $
40.00.
El procedimiento
anterior es mucho más sencillo y se basa en la representación
decimal de los porcentajes.
Encontrar el porcentaje de un número
Para
determinar el porcentaje de un número sigue los siguientes
pasos:
-
Multiplica el número por el porcentaje (ej. 87 X 68 =
5916)
-
Divide
el resultado por 100 (Mueve el punto decimal dos lugares
hacia la izquierda) (ej. 5916/100 = 59.16)
-
Redondea
a la precisión deseada (ej. 59.16 redondeado al número
entero más próximo = 59)
Ejemplo: ¿68
que porcentaje es de 87?
-
Divide
el primer número por el Segundo (ej. 68 ÷ 87 = 0.7816)
-
Multiplica el resultado por 100 (Mueve el punto decimal
dos lugares hacia la derecha) (ej. 0.7816 X 100 = 78.16)
-
Redondea
con la precisión deseada (ej. 78.16 redondeado al número
entero más próximo = 78)
-
Termina
tu respuesta con el signo % ej. 68 es el 78% de 87)
Convertir una fracción a un porcentaje
Sigue los
siguientes pasos para convertir una fracción a un porcentaje.
Por ejemplo: Convierte 4/5 a un porcentaje.
-
Divide
el numerador de la fracción por el denominador ( ej. 4 ÷
5 = 0.80)
-
Multiplica por 100 (Mueve el punto decimal dos lugares
hacia la derecha)
-
(ej.
0.80 X 100=80)
-
Redondea
el resultado a la precisión deseada.
-
Termina
tu respuesta con el signo % (ej. 80%)
Convertir un porcentaje a una fracción
Sigue los
siguientes pasos para convertir un porcentaje a una fracción:
Por ejemplo: Convierte 83% a una fracción.
-
Elimina el signo porcentual
-
Haz
una fracción con el porcentaje como el numerador y 100
como el denominador (ej. 83/100).
-
De ser
necesario reduce la fracción.
Experimentos
aleatorios
Los experimentos
aleatorios, osea, regidos por el azar,
son aquellos en que se verifican los dos puntos
siguientes: se pueden repetir indefinidamente,
siempre en las mismas condiciones, y antes de
realizar el experimento, se conocen todos los
resultados posibles, pero no es posible tener
certeza de cual será el resultado del
experimento.
Veamos el siguiente ejemplo: el
lanzamiento de un dado.
El lanzamiento de un dado es un experimento
aleatorio, ya que, se cumplen los dos puntos
mencionados anteriormente: el experimento lo
podemos repetir cuantas veces queramos en las
mismas condiciones y conocemos todos los
resultados posibles, a pesar de no tener la
certeza de qué resultados obtendremos.
Todos los resultados posibles de nuestro
experimento son los siguientes:
- Que salga 1
- Que salga 2
- Que salga 3
- Que salga 4
- Que salga 5
- Que salga 6
A todos los resultados posibles de un
experimento aleatorio se le denomina
espacio muestral.
En nuestro ejemplo: E = {1, 2, 3 ,4, 5,
6}
Llamaremos evento o
suceso a todo subconjunto de un espacio
muestral.
Ejemplos:
Obtener un número mayor o igual a 5: A = {5, 6}
Obtener un número par: B = {2, 4, 6}
La probabilidad de ocurrencia de un evento
determinado, es decir, el nivel de certeza que
tenemos de que ocurra dicho suceso, es la razón
entre el número de veces en que ocurrió dicho
evento y el número de repeticiones del
experimento. A esta razón se le denomina
frecuencia relativa.

De acuerdo al valor de la frecuencia relativa
podemos encontrar eventos seguros, posibles o
probables e imposibles:
Evento seguro
Es aquel cuya probabilidad de ocurrencia es
igual a 1.
Calculemos la probabilidad de obtener un número
menor que 7 al lanzar un dado. Supongamos que
realizamos el experimento 10 veces:

Es seguro que obtendremos un
número menor que 7 al lanzar un dado cuantas
veces queramos.
Evento Imposible
Es aquel cuya probabilidad de ocurrencia es
igual a 0.
Obtengamos la probabilidad de obtener un 8 al
lanzar un dado 12 veces:

Es imposible obtener un 8 al
lanzar un dado, aunque repitamos el experimento
infinitas veces.
Evento posible o probable
Es aquel cuya probabilidad de ocurrencia se
encuentra entre 0 y 1. Cuanto menos probable sea
el suceso, más cerca estará del 0 y cuanto más
probable sea, más cerca estará del 1.
Calculemos la probabilidad de obtener un 3 si
suponemos que lanzamos un dado 12 veces y
obtenemos los siguientes resultados: 3 veces
obtuvimos un 1, 1 vez un 2, 1 vez un 3, 2 veces
un 4, 3 veces un 5 y 2 veces un 6.

Es probable que al lanzar 12
veces un dado, obtengamos como resultado un
número 3.
Repetición de un experimento
Mientras más veces repitamos un experimento,
mejor será la estimación de los resultados que
obtendremos.
Por ejemplo, si lanzamos 100 veces una moneda,
el número de veces que obtengo cara será cercano
a 50, o sea, la frecuencia relativa será cercana
a:
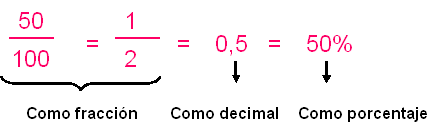
En nuestro experimento de lanzamiento de un
dado, mientras más veces lo repitamos, veremos
que la frecuencia relativa, es decir, la
probabilidad de ocurrencia de obtener un 1, un
2, un 3, un 4, un 5 o un 6 será cercana al
16,7%.
Si lanzamos el dado 600
veces, el número de veces que obtendremos cada
uno de los 6 posibles números será cercano a
100, por lo que la frecuencia relativa será
cercana a:
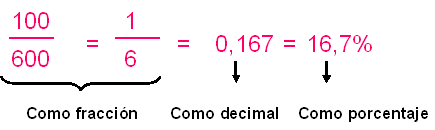
WWW.PROYECTOSALONHOGAR.COM |
|

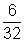 y al simplificar se tiene,
y al simplificar se tiene,
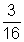 es decir, que reprobaron
español 3 de cada 16 alumnos.
es decir, que reprobaron
español 3 de cada 16 alumnos. 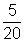 Esta es la representación en forma de razón que simplificada
queda
Esta es la representación en forma de razón que simplificada
queda 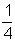 Dicho de otra forma;
1 persona de cada 4 pasó a la final.
Dicho de otra forma;
1 persona de cada 4 pasó a la final.