| |
|
L a G r a n E n
c i c l o p e d i a I l u s t r a d a d e l
P r o y e c t o S a l ó n H o g a r |
|
|

La
Estadistica y la probabilidad
Cómo calcular la media
El valor medio (también se
llama la media) es simplemente el promedio
de los números.
Es fácil de calcular: sólo
suma los números, después divide por
cuántos números hay. (En otras palabras es
la suma dividida por la cuenta).
Ejemplo 1:
¿Cuál es la media de estos
números?
3, 10, 5
Suma los números: 3 + 10 +
5 = 18
Divide por cuántos números hay (tenemos 3
números): 18 ÷ 3 = 6
La
media es 6
Ejemplo 2:
Mira estos números:
3, 7, 5, 13, 20, 23,
39, 23, 40, 23, 14, 12, 56, 23, 29
La suma de estos números
es igual a 330
Hay quince números.
La media es igual a 330 ÷
15 = 22
El
valor medio de los números de arriba es 22
Números
negativos
¿Qué hacemos con los
números negativos? Sumar un número negativo es
lo mismo que restarlo (quitándole el signo
menos). Por ejemplo 3 + (-2) = 3-2 = 1. Sabiendo
esto, vamos a hacer un ejemplo:
Ejemplo 3:
Calcula la media de estos
números:
3, -7, 5, 13, -2
La suma de estos números
es 3-7+5+13-2 = 12
Hay 5 números.
La media es igual a 12 ÷ 5
= 2.4
La
media de los números de arriba es 2.4
|
|
Cómo calcular la mediana
Es el número en el
medio de una lista ordenada.
Para calcular la mediana, ordena los números que
te han dado según su valor y encuentra
el que queda en el medio.
Mira estos números:
3, 13, 7, 5, 21, 23, 39,
23, 40, 23, 14, 12, 56, 23, 29
Si los ordenamos queda:
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29,
39, 40, 56
Hay quince
números. El del medio es el octavo
número:
3, 5, 7, 12, 13, 14,
21, 23, 23,
23, 23, 29, 39, 40, 56
La mediana de este
conjunto de valores es 23.
(Fíjate en que no importan
mucho los otros números de la lista)
PERO si hay una
cantidad par de números la cosa cambia un
poco.
En ese caso tenemos que encontrar el par
central de números, y después calcular su
valor medio. Esto se hace simplemente sumándolos
y dividiendo entre dos.
Lo vemos mejor con un ejemplo:
3, 13, 7, 5, 21, 23, 23,
40, 23, 14, 12, 56, 23, 29
Si ordenamos los
números nos queda:
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29,
40, 56
Ahora hay catorce
números así que no tenemos sólo uno en el
medio, sino un par:
3, 5, 7, 12, 13, 14,
21,
23, 23, 23, 23,
29, 40, 56
En este ejemplo los
números intermedios son 21 y 23.
Para calcular el valor
en medio de ellos, sumamos y dividimos entre
2:
21 + 23 = 44
44 ÷ 2 = 22
Así que la mediana
en este ejemplo es 22.
|
|
Cómo calcular la moda o valor modal
La moda es simplemente el
valor que aparece más veces.
Para calcular la moda
tienes que ordenar los números que te dan.
Mira estos números:
3, 7, 5, 13, 20, 23, 39, 23,
40, 23, 14, 12, 56, 23, 29
Ordenados quedan:
3, 5, 7, 12, 13, 14, 20, 23,
23, 23, 23, 29, 39, 40, 56
Así es más fácil ver qué
números aparecen más veces.
En este
caso la moda es 23. |
|
Línea de
probabilidades
La probabilidad indica lo
fácil que es que algo pase. Se puede usar
una línea para representarla.
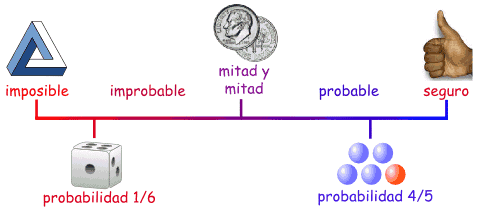
Podemos decir que la
probabilidad de que algo pase está entre
imposible y seguro.
Además de usar palabras se
pueden usar fracciones o decimales para indicar
la probabilidad de que algo pase. Imposible es
cero y seguro es uno. Aquí tienes
una línea de probabilidades con fracciones.
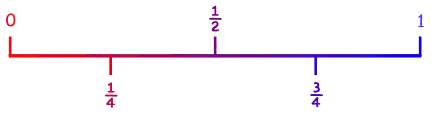
Podemos indicar con ella
la probablidad de que algo pase:
a) El sol salga mañana.
b) No tenga que aprender matemáticas.
c) Si tiro una moneda saldrá cara.
d) Si doy a alguien a elegir entre rojo,
amarillo, azul o verde, elegirá rojo.
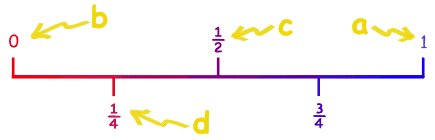
Recuerda que la probabilidad
nunca vale más de 1.
Esto es porque vale 1 cuando algo es seguro.
Y la
probabilidad nunca vale menos de 0.
Esto es porque vale 0 cuando algo es imposible
(seguro que no pasa).
|
|
Exactitud y precisión
¡Significan cosas
un poco distintas!
Exactitud
La exactitud es lo cerca que
el resultado de una medición está del valor
verdadero.
Precisión
La precisión es lo cerca que
los valores medidos están unos de otros.
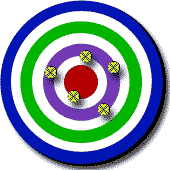
Ejemplos de
exactitud y precisión:
 |
 |
 |
Exactitud
baja
Precisión alta |
Exactitud
alta
Precisión baja |
Exactitud
alta
Precisión alta |
Así que si estás jugando
al fútbol y siempre le das al poste izquierdo en
lugar de marcar gol, ¡entonces no eres
exacto, pero eres preciso!
Sesgo (¡que no
te engañe la precisión!)
Así que si medimos algo
varias veces y los valores están cerca unos de
otros, pueden estar todos equivocados si
hay "sesgo".
Un sesgo es un
error sistemático (pasa siempre) que hace que
todas las medidas estén desviadas en una cierta
cantidad.
Ejemplos de
sesgos
- Un balanza dice "1 kg"
cuando no hay ningún peso encima
- Siempre mides tu
altura con zapatos de suelas anchas
- Un cronómetro que se
para medio segundo después de pulsar el
botón
Grado de
exactitud
La exactitud depende del
instrumento de medida. Pero por regla general:
El grado de exactitud
es la mitad de la unidad de medida.
Ejemplos:
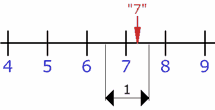
| Si tu
instrumento mide en "unidades"
entonces cualquier valor entre 6½
y 7½ se mide como "7" |
 |
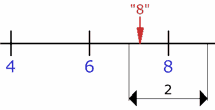
| Si tu
instrumento mide "de 2 en 2"
entonces los valores entre 7
y 9 dan medida "8" |
 |
|
|
Varianza y desviación estándar
La
desviación sólo significa qué tan lejos de lo
normal
Desviación estándar
La desviación estándar (σ)
mide cuánto se separan los datos.
La fórmula es fácil: es la
raíz cuadrada de la varianza. Así que,
"¿qué es la varianza?"
Varianza
la varianza (que es el
cuadrado de la desviación estándar: σ2)
se define así:
Es la media de las
diferencias con la media elevadas al cuadrado.
En otras palabras, sigue
estos pasos:
1. Calcula la media (el
promedio de los números)
2. Ahora, por cada número resta la media y eleva
el resultado al cuadrado (la diferencia elevada
al cuadrado).
3. Ahora calcula la media de esas diferencias al
cuadrado. (¿Por qué al cuadrado?)
Ejemplo
Tú y tus amigos habéis
medido las alturas de vuestros perros (en
milímetros):
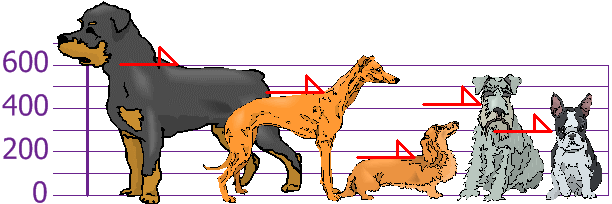
Las alturas (de los
hombros) son: 600mm, 470mm, 170mm, 430mm y
300mm.
Calcula la media, la
varianza y la desviación estándar.
Respuesta:
| Media
= |
600 + 470 + 170 +
430 + 300
|
= |
1970
|
=
394 |
|
|
|
|
5
|
5
|
así que la altura media es
394 mm. Vamos a dibujar esto en el gráfico:
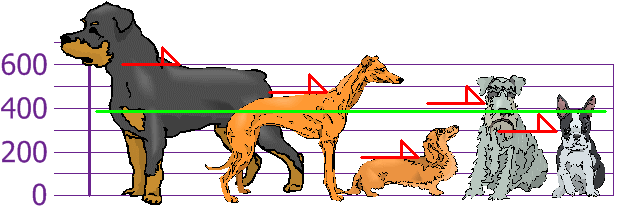
Ahora calculamos la
diferencia de cada altura con la media:
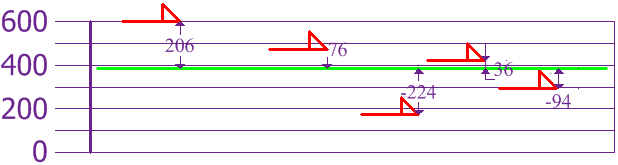
Para calcular la varianza,
toma cada diferencia, elévala al cuadrado, y haz
la media:
|
Varianza: σ2 = |
2062 +
762 + (-224)2
+ 362 + (-94)2
|
= |
108,520
|
=
21,704 |
|
|
|
|
5
|
5
|
Así que la varianza es
21,704.
Y la desviación estándar
es la raíz de la varianza, así que:
Desviación estándar: σ
= √21,704 = 147
y lo bueno de la
desviación estándar es que es útil: ahora
veremos qué alturas están a distancia menos de
la desviación estándar (147mm) de la media:
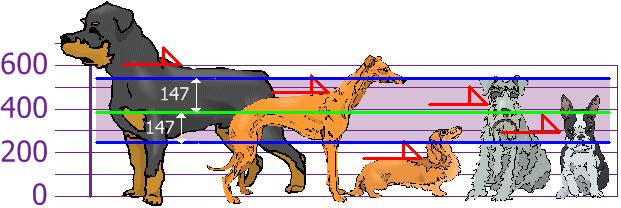
Así que usando la
desviación estándar tenemos una manera
"estándar" de saber qué es normal, o extra
grande o extra pequeño.
Los Rottweilers son
perros grandes. Y los Dachsunds son un
poco menudos... ¡pero que no se enteren!
*Nota: ¿por qué
al cuadrado?
Elevar cada diferencia al
cuadrado hace que todos los números sean
positivos (para evitar que los números negativos
reduzcan la varianza)
Y también hacen que las
diferencias grandes se destaquen. Por ejemplo
1002=10,000 es mucho más grande que
502=2,500.
Pero elevarlas al cuadrado
hace que la respuesta sea muy grande, así que lo
deshacemos (con la raíz cuadrada) y así la
desviación estándar es mucho más útil. |
|
WWW.PROYECTOSALONHOGAR.COM |
|