La
Estadística es una disciplina que utiliza recursos matemáticos
para organizar y resumir una gran cantidad de datos obtenidos de la
realidad, e inferir conclusiones respecto de ellos.
 Introducción:
La estadística es una rama de
la Matemática que se ocupa de la recolección, organización,
análisis e interpretación de datos. La información contenida
en una gran cantidad de datos recolectados es muy difícil de
obtener si no se realizan antes las tareas de organización,
análisis e interpretación propios de la Estadística.
Es por esto que en muchas áreas del conocimiento,
actualmente la Estadística resulta muy útil, y en algunas,
hasta indispensable. Por ejemplo, en las Ciencias Sociales
se requiere con frecuencia estudiar el comportamiento o la
situación de grupos humanos numerosos, y para ello, la
Estadística resulta ser una herramienta fundamental.
|
Definiciones Básicas:
Con el objeto de definir algunos de los términos elementales
que se usan en Estadística, se planteará el estudio de un
fenómeno en particular, desde el punto de vista estadístico.
Supóngase que se desea estudiar el fenómeno del rendimiento
académico de los estudiantes de
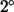año de Ciencias de un cierto colegio, en la asignatura de
Física.
|
Población:
Se denomina 'población' del estudio
estadístico, en este caso, al grupo de todos los estudiantes
de
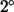año de Ciencias del colegio en cuestión. Es importante
observar que la palabra 'población', en Estadística, puede
referirse a un conjunto de objetos y no necesariamente a un
conjunto de personas o seres vivos en general. Por ejemplo,
si se quiere hacer un estudio del estado en que se
encuentran los pupitres de todo el colegio, clasificándolos
en tres categorías: inservible, reparable, y en buenas
condiciones, en este caso la población estaría conformada
por todos los pupitres que hay en el colegio.
|
Muestra:
Cuando la población es muy numerosa, se hace
difícil obtener y analizar la información proveniente de
todos los individuos, y en ese caso se seleccionan algunos
individuos representativos de la población para hacer el
estudio estadístico. El grupo de individuos seleccionados se
denomina muestra. En el caso del estudio sobre el
rendimiento académico de los esudiantes de
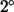año de Ciencias, si se tratara de un colegio pequeño con
sólo una sección de cada curso, se tomaría toda la población
para el estudio. Pero si se tratara de un colegio muy grande,
con 10 secciones de
año de Ciencias, probablemente se tomaría una muestra,
seleccionando unos 5, 10 ó 12 estudiantes de cada sección,
según las posibilidades del equipo que realiza el estudio.
|
Variables estadísticas:
Las variables estadísticas son los
datos que proporcionan los individuos de la población (o
muestra) observada. Pueden ser cuantitativas, como en el
caso del estudio del rendimiento académico, si se usa el
dato de la nota definitiva que obtuvo cada alumno en la
asignatura de Física. Siempre que la información esté dada a
través de números, se considera que es una vairable
cuantitativa. En el caso del estudio sobre el estado de los
pupitres del colegio, se tiene una variable cualitativa,
pues la información sobre cada pupitre no está dada en
términos numéricos, sino que se ubica a cada uno en una de
las categorías: inservible, reparable, en buenas condiciones.
|
Organización de Datos:
Se obtienen los siguientes datos al
investigar acerca de las notas obtenidas en Física por los
35 estudiantes de
año de Ciencias: 12, 06, 18, 10, 11, 11, 17, 09, 07, 10, 09,
15, 13, 03, 16, 12, 16, 10, 08, 05, 10, 13, 18, 11, 12, 03,
07, 09, 20, 14, 16, 10, 04, 09, 18. Un primer paso a tomar
para la organización de esta información, de manera que se
facilite su estudio, es el siguiente: se construye una tabla
estadística, llamada tabla de frecuencias, en la cual se
apreciará el número de estudiantes que obtuvo cada nota,
desde 0 hasta 20:
|
A partir de esta tabla se pueden obtener representaciones
gráficas del fenómeno estudiado, como por ejemplo un
histograma, que se construirá más adelante. Sin embargo, hay
varios aspectos del rendimiento académico del curso
observado, que se hacen evidentes al organizar los datos
como en la tabla anterior. Por ejemplo, el número de alumnos
que tienen una nota inferior a 07 es 5 (2 sacaron 03, 1 sacó
04, 1 sacó 05 y 1 sacó 06). De estos 5 alumnos se puede
decir que no aprendieron lo que se esperaba durante el curso.
|
Medio
estadístico
El medio estadístico es
comunmente llamando promedio:
Para averiguar el medio de un
grupo de números:
- Suma los números todos
juntos
- Divide por la cantidad de
números que fueron sumados
Mediana
estadística
La mediana estadística es el
número central de un grupo de números ordenados por tamaño. Si
la cantidad de términos es par, la mediana es el promedio de los
dos números centrales:
Para averiguar la mediana de un
grupo de números:
- Ordena los números según
su tamaño
- Si la cantidad de términos
es impar, la mediana es el valor central.
- Si la cantidad de términos
es par, suma los dos términos del medio y divide por 2.
Rango
estadístico
El rango estadístico es la
diferencia entre el valor mínimo y el valor máximo en un grupo
de números.
Para averiguar el rango de un
grupo de números:
- Ordena los números según
su tamaño
- Resta el valor mínimo del
valor máximo.
Moda
estadística
La moda estadística es el valor
que más se repite en un grupo de números.
Para averiguar la moda en un
grupo de números:
- Ordena los números según
su tamaño.
- Determina la cantidad de
veces de cada valor numérico.
- El valor numérico que más
se repite es la moda.
- Puede haber más de una
moda cuando dos o más números se repiten la misma cantidad
de veces y además este es el máximo número de veces del
conjunto.
- No hay moda si ningún
número se repite más de una vez.
Ejemplo: La moda de 2, 4, 5, 5,
5, 7, 8, 8, 9, 12 es 5.
Medio
estadístico
El medio estadístico es
comunmente llamando promedio:
Para averiguar el medio de un
grupo de números:
- Suma los números todos
juntos
- Divide por la cantidad de
números que fueron sumados
Mediana
estadística
La mediana estadística es el
número central de un grupo de números ordenados por tamaño. Si
la cantidad de términos es par, la mediana es el promedio de los
dos números centrales:
Para averiguar la mediana de un grupo de números:
- Ordena los números según
su tamaño
- Si la cantidad de términos
es impar, la mediana es el valor central.
- Si la cantidad de términos
es par, suma los dos términos del medio y divide por 2.
Rango
estadístico
El rango estadístico es la
diferencia entre el valor mínimo y el valor máximo en un grupo
de números.
Para averiguar el rango de un
grupo de números:
- Ordena los números según
su tamaño
- Resta el valor mínimo del
valor máximo.
Medio
estadístico
El medio estadístico es
comunmente llamando promedio:
Para averiguar el medio de un
grupo de números:
- Suma los números todos
juntos
- Divide por la cantidad de
números que fueron sumados
Mediana
estadística
La mediana estadística es el
número central de un grupo de números ordenados por tamaño. Si
la cantidad de términos es par, la mediana es el promedio de los
dos números centrales:
Para averiguar la mediana de un grupo de números:
- Ordena los números según
su tamaño
- Si la cantidad de términos
es impar, la mediana es el valor central.
- Si la cantidad de términos
es par, suma los dos términos del medio y divide por 2.
Rango
estadístico
El rango estadístico es la
diferencia entre el valor mínimo y el valor máximo en un grupo
de números.
Para averiguar el rango de un
grupo de números:
- Ordena los números según
su tamaño
- Resta el valor mínimo del
valor máximo.
Principio básico
de conteo
El principio básico o
fundamental de conteo se puede utilizar para determinar los
posibles resultados cuando hay dos o más características que
pueden variar.
Ejemplo: El helado puede venir
en un cono o una tasa y los sabores son chocolate, fresa y
vainilla.
/ tasa de chocolate
/ chocolate <
/ \ cono de chocolate
/
/ / tasa de fresa
<-- fresa <
\ \ cono de fresa
\
\ / tasa de vainilla
\ vainilla <
\ cono de vainilla
El diagrama anterior se llama
diagrama de árbol y muestra todas las posibilidades. El diagrama
de árbol también se puede ordenar de otra forma. Ambos diagramas
tienen un total de 6 resultados.
/ tasa de chocolate
/
/ tasa <-- tasa de fresa
/ \
/ \ tasa de vainilla
/
<
\
\ / cono de chocolate
\ /
\ cono <-- cono de fresa
\
\ cono de vainilla
Para determinar la cantidad
total de resultados, multiplica la cantidad de posibilidades de
la primera característica por la cantidad de posibilidades de la
segunda característica. En el ejemplo anterior, multiplica 3 por
2 para obtener 6 posibles resultados.
Si hay más de dos resultados,
continúa multiplicando las posibilidades para determinar el
total de resultados.
Factoriales
Un factorial se
designa con un número natural positivo seguido por un signo de
exclamación (es decir 8!). El valor de un factorial es el
producto de todos los números desde 1 hasta el número del
factorial. 8! = 1 x 2 x 3 x 4 x 5 x 6 x 7x 8 = 40,320. Los
factoriales se utilizan para determinar las cantidades de
combinaciones y permutaciones y para averiguar probabilidades.
Permutaciones
Una permutación es una
combinación en donde el orden es importante. La notación para
permutaciones es P(n,r) que es la cantidad de permutaciones de
“n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes
toman un examen y todos obtienen diferente calificación,
cualquier alumno podría alcanzar la calificación más alta. La
segunda calificación más alta podría ser obtenida por uno de los
8 restantes. La tercera calificación podría ser obtenida por uno
de los 7 restantes.
La cantidad de permutaciones
posibles sería: P(9,3) = 9x8x7 = 504 combinaciones posibles de
las tres calificaciones más altas.
Combinaciones
Una combinación es un arreglo
donde el orden NO es importante. La notación para las
combinaciones es C(n,r) que es la cantidad de combinaciones de
“n” elementos seleccionados, “r” a la vez. Es igual a la
cantidad de permutaciones de “n” elementos tomados “r” a la vez
dividido por “r” factorial. Esto sería P(n,r)/r! en notación
matemática.
Ejemplo: Si se seleccionan
cinco cartas de un grupo de nueve, ¿cuantas combinaciones de
cinco cartas habría?
La cantidad de combinaciones
posibles sería: P(9,5)/5! = (9x8x7x6x5)/(5x4x3x2x1) = 126
combinaciones posibles.
Probabilidad
simple
| |
Cantidad de formas en
que un resultado específico va a suceder |
| Probabilidad = |
|
| |
Cantidad total de
posibles resultados |
Ejemplo: Hay 87 canicas en una
bolsa y 68 son verdes. Si se escoge una, ¿cuál es la
probabilidad de que esta sea verde?
Solución:
- Divide la cantidad de
formas de elegir una canica verde (68) por la cantidad total
de canicas (87)
- 68 ÷ 87 = 0.781609
- Redondea a la precisión
deseada (es decir 0.781609 redondeado a centésimos es 0.78)
Cómo
calcular la media
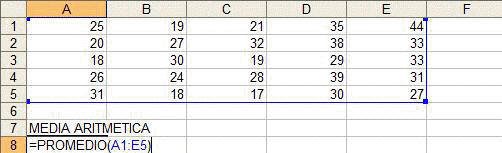
El valor medio (también se llama la
media) es simplemente el promedio de los números.
Es fácil de calcular: sólo suma
los números, después divide por cuántos números hay. (En
otras palabras es la suma dividida por la cuenta).
Ejemplo 1:
¿Cuál es la media de estos números?
3, 10, 5
Suma los números: 3 + 10 + 5 = 18
Divide por cuántos números hay (tenemos 3 números): 18 ÷ 3 =
6
La media es 6
Ejemplo 2:
Mira estos números:
3, 7, 5, 13, 20, 23, 39, 23,
40, 23, 14, 12, 56, 23, 29
La suma de estos números es igual a
330
Hay quince números.
La media es igual a 330 ÷ 15 = 22
El valor medio de los
números de arriba es 22
Números negativos
¿Qué hacemos con los números
negativos? Sumar un número negativo es lo mismo que restarlo (quitándole
el signo menos). Por ejemplo 3 + (-2) = 3-2 = 1. Sabiendo esto,
vamos a hacer un ejemplo:
Ejemplo 3:
Calcula la media de estos números:
3, -7, 5, 13, -2
La suma de estos números es
3-7+5+13-2 = 12
Hay 5 números.
La media es igual a 12 ÷ 5 = 2.4
La media de los números
de arriba es 2.4
Cómo calcular la
mediana
Es el número en el medio de una
lista ordenada.
Para calcular la mediana, ordena los números que te han dado
según su valor y encuentra el que queda en el medio.
Mira estos números:
3, 13, 7, 5, 21, 23, 39, 23, 40,
23, 14, 12, 56, 23, 29Si
los ordenamos queda:
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56
Hay quince números. El
del medio es el octavo número:
3, 5, 7, 12, 13, 14, 21,
23, 23, 23, 23, 29, 39, 40, 56
La mediana de este conjunto de
valores es 23.
(Fíjate en que no importan mucho
los otros números de la lista)
PERO si hay una cantidad par de
números la cosa cambia un poco.
En ese caso tenemos que encontrar el par central de números,
y después calcular su valor medio. Esto se hace simplemente
sumándolos y dividiendo entre dos.
Lo vemos mejor con un ejemplo:
3, 13, 7, 5, 21, 23, 23, 40, 23,
14, 12, 56, 23, 29
Si ordenamos los números nos
queda:
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 40, 56
Ahora hay catorce
números así que no tenemos sólo uno en el medio, sino un par:
3, 5, 7, 12, 13, 14,
21, 23,
23, 23, 23, 29, 40, 56
En este ejemplo los números
intermedios son 21 y 23.
Para calcular el valor en medio
de ellos, sumamos y dividimos entre 2:
21 + 23 = 44
44 ÷ 2 = 22
Así que la mediana en
este ejemplo es 22.
Cómo calcular la
moda o valor modal
La moda es simplemente el valor que
aparece más veces.
Para calcular la moda tienes que
ordenar los números que te dan.
Mira estos números:
3, 7,
5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29
Ordenados
quedan:
3, 5,
7, 12, 13, 14, 20, 23, 23, 23, 23, 29, 39, 40, 56
Así es más fácil ver qué números
aparecen más veces.
En este caso la moda
es 23.
Línea
de probabilidades
La probabilidad indica lo
fácil que es que algo pase. Se puede usar una línea para
representarla.
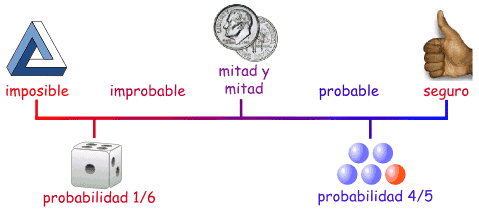
Podemos decir que la probabilidad
de que algo pase está entre imposible y seguro.
Además de usar palabras se pueden
usar fracciones o decimales para indicar la probabilidad de que algo
pase. Imposible es cero y seguro es uno. Aquí tienes
una línea de probabilidades con fracciones.
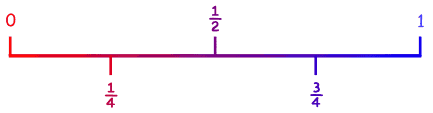
Podemos indicar con ella la
probablidad de que algo pase:
a) El sol salga mañana.
b) No tenga que aprender matemáticas.
c) Si tiro una moneda saldrá cara.
d) Si doy a alguien a elegir entre rojo, amarillo, azul o verde,
elegirá rojo.
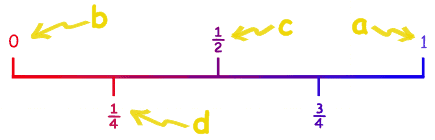
Recuerda que la
probabilidad nunca vale más de 1.
Esto es porque vale 1 cuando algo es seguro.
Y la probabilidad
nunca vale menos de 0.
Esto es porque vale 0 cuando algo es imposible (seguro que no pasa).
Exactitud y
precisión
¡Significan cosas un
poco distintas!
Exactitud
La exactitud es lo cerca que el
resultado de una medición está del valor verdadero.
Precisión
La precisión es lo cerca que los
valores medidos están unos de otros.
Ejemplos de
exactitud y precisión:
 |
 |
 |
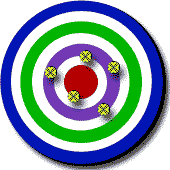Exactitud baja
Precisión alta |
Exactitud
alta
Precisión baja |
Exactitud alta
Precisión alta |
Así que si estás jugando al fútbol
y siempre le das al poste izquierdo en lugar de marcar gol, ¡entonces
no eres exacto, pero eres preciso!
Sesgo (¡que no te engañe la
precisión!)
Así que si medimos algo varias
veces y los valores están cerca unos de otros, pueden estar
todos equivocados si hay "sesgo".
Un sesgo es un error
sistemático (pasa siempre) que hace que todas las medidas estén
desviadas en una cierta cantidad.
Ejemplos de sesgos
- Un balanza dice "1 kg" cuando
no hay ningún peso encima
- Siempre mides tu altura con
zapatos de suelas anchas
- Un cronómetro que se para
medio segundo después de pulsar el botón
Grado de exactitud
La exactitud depende del
instrumento de medida. Pero por regla general:
El grado de exactitud es
la mitad de la unidad de medida.
Ejemplos:
| Si tu
instrumento mide en "unidades" entonces cualquier valor
entre 6½ y 7½ se mide como
"7" |
 |
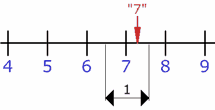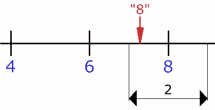
| Si tu
instrumento mide "de 2 en 2" entonces los valores entre
7 y 9 dan medida
"8" |
 |
Varianza y desviación estándar
La desviación
sólo significa qué tan lejos de lo normal
Desviación estándar
La desviación estándar (σ)
mide cuánto se separan los datos.
La fórmula es fácil: es la raíz
cuadrada de la varianza. Así que, "¿qué es la varianza?"
Varianza
la varianza (que es el cuadrado de
la desviación estándar: σ2) se define así:
Es la
media de las diferencias con la media elevadas al cuadrado.
En otras palabras, sigue estos
pasos:
1. Calcula la media (el
promedio de los números)
2. Ahora, por cada número resta la media y eleva el resultado al
cuadrado (la diferencia elevada al cuadrado).
3. Ahora calcula la media de esas diferencias al cuadrado. (¿Por qué
al cuadrado?) VER ABAJO
Ejemplo
Tú y tus amigos habéis medido las
alturas de vuestros perros (en milímetros):
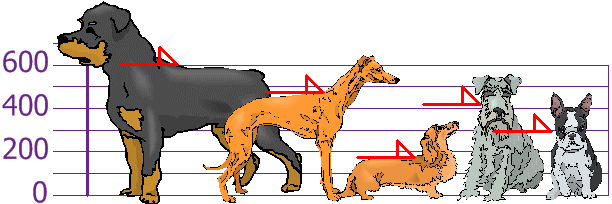
Las alturas (de los hombros) son:
600mm, 470mm, 170mm, 430mm y 300mm.
Calcula la media, la varianza y la
desviación estándar.
Respuesta:
| Media = |
600 + 470 + 170 + 430 +
300
|
= |
1970
|
= 394 |
|
|
|
|
5
|
5
|
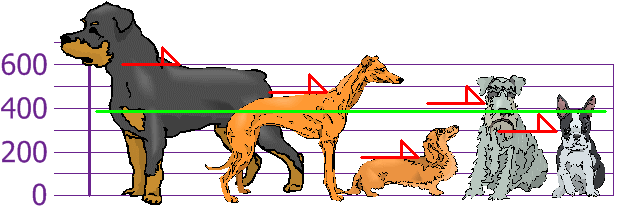
así que la altura media es 394 mm.
Vamos a dibujar esto en el gráfico:
Ahora calculamos la diferencia de
cada altura con la media:
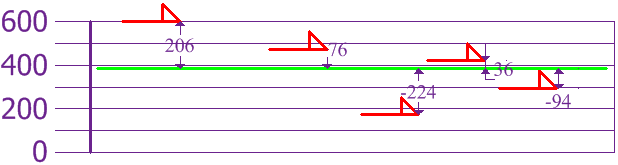
Para calcular la varianza, toma
cada diferencia, elévala al cuadrado, y haz la media:
| Varianza: σ2
= |
2062 + 762
+ (-224)2 + 362 + (-94)2
|
= |
108,520
|
= 21,704 |
|
|
|
|
5
|
5
|
Así que la varianza es 21,704.
Y la desviación estándar es la raíz
de la varianza, así que:
Desviación estándar:
σ = √21,704 = 147
y lo bueno de la desviación
estándar es que es útil: ahora veremos qué alturas están a distancia
menos de la desviación estándar (147mm) de la media:
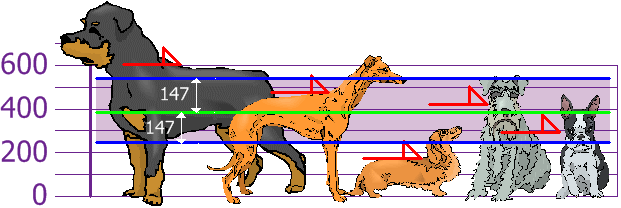
Así que usando la desviación
estándar tenemos una manera "estándar" de saber qué es normal, o
extra grande o extra pequeño.
Los Rottweilers son perros
grandes. Y los Dachsunds son un poco menudos... ¡pero que no
se enteren!
*Nota: ¿por qué al cuadrado?
Elevar cada diferencia al cuadrado
hace que todos los números sean positivos (para evitar que los
números negativos reduzcan la varianza)
Y también hacen que las diferencias
grandes se destaquen. Por ejemplo 1002=10,000 es mucho
más grande que 502=2,500.
Pero elevarlas al cuadrado hace que
la respuesta sea muy grande, así que lo deshacemos (con la raíz
cuadrada) y así la desviación estándar es mucho más útil.
|
