(Euclid, Book VII. Def.20.)
That is the ratio -- the relationship -- of 15 to 5. If Jill has $15, and Jack has $5, then Jill has three times more than Jack.
We do not answer "3 to 1," because we want to name the ratio of 15 to 5 explicitly. It is true that 15 is to 5 as 3 is to 1 -- but what ratio has 3 to 1? 3 is three times 1.
(The 19th century program to rid mathematics of language and replace it with algebraic relations, successfully put to sleep the subject of ratio and proportion.)
Notice that we answer with a complete sentence beginning with the first number 15 and ending with the last number 5. For, a ratio is a relationship.
The two numbers in a ratio are called the terms; the first and the second.
When the first term is larger, we say it is so many times the smaller number. 15 is three times 5.
What ratio has 28 to 7?
28 is four times 7.
Example 2. Part. What ratio has 5 to 15?
Answer. 5 is the third part of 15.
That is called the inverse ratio of 15 to 5. The terms are exchanged.
Notice again that we answer with a complete sentence beginning with the first term and ending with the second. "5 is 15."
Example 3. Parts. What ratio has 10 to 15?
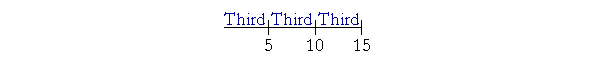
Answer. 10 is two thirds of 15.
These are the three types of ratio. One number is a multiple of the other (so many times it), a part of it, or parts of it.
Example 4. What ratio has 12 to 6?
Answer. 12 is two
times 6. Or we could say, "12 is twice as much as 6," or "12 is double 6."
These are the various ways of expressing the ratio, the relationship, of 12 to 6.
Inversely, 6 is half of 12.
When trying to express a ratio, if the student will say a sentence, and then consider the truth of that sentence, the fact will speak for itself.
Example 5. What ratio has 6 to 30? And inversely, what ratio has 30 to 6?
Answer. 6 is the fifth part of 30. Inversely, 30 is five times 6.
Example 6. What ratio has 63 to 7? And inversely, what ratio has 7 to 63?
Answer. 63 is nine times 7. Inversely, 7 is the ninth part of 63.