2
LIMITS
A sequence of rational numbers
Left-hand and right-hand limits
The definition of the limit of a variable
CENTRAL TO CALCULUS is the idea of a limit. And central to the idea of a limit is the idea of a sequence of rational numbers.
A sequence of rational numbers
In geometry we encounter such a sequence when we determine the area
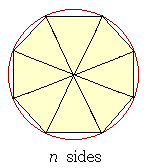 of a circle. To do that, we inscribe in the circle a regular polygon of n sides. As the number of sides increases -- that is, if we consider a sequence of polygons: 60 sides, 61 sides, 62, 63, 64, and so on -- then the sequence of areas of the polygons gets closer and closer to the area of the circle. The area of the circle is their limit. Now, the circle is never equal to a polygon. But by taking n to be a sufficiently large number, the difference between the circle and a polygon will be less than any small number we name. Less even than
of a circle. To do that, we inscribe in the circle a regular polygon of n sides. As the number of sides increases -- that is, if we consider a sequence of polygons: 60 sides, 61 sides, 62, 63, 64, and so on -- then the sequence of areas of the polygons gets closer and closer to the area of the circle. The area of the circle is their limit. Now, the circle is never equal to a polygon. But by taking n to be a sufficiently large number, the difference between the circle and a polygon will be less than any small number we name. Less even than
0.00000000000000000000000000000001![]()
That is the idea of a sequence approaching a limit.
Problem 1. The student surely can recognize the number that is the limit of this sequence of rational numbers.
3, 3.1, 3.14, 3.141, 3.1415, 3.14159, 3.141592, . . .
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
π
Every irrational number is in fact the limit of a sequence of rational numbers. And again, the limit is not a member of the sequence. (The irrational number "exists" only as a limit.)
We speak of a sequence as being infinite, which is a brief way of saying that, no matter how many terms there are, we could always add one more. And when the sequence has a limit, each term we add will be closer to the limit than the previous term.
The limit of a variable
Consider this sequence of values of a variable x:
1.9, 1.99, 1.999, 1.9999, 1.99999, . . .
These values are getting closer and closer to 2 -- they are approaching 2 as their limit. 2 is the smallest number such that every member of that sequence will be less.
We can define "closer and closer" mathematically as follows. We can say that the differences between the terms of that sequence and 2 become and remain less than any small number we might name. That is, we can define a limit by considering the sequence of differences, x − 2 :
1.9 − 2, 1.99 − 2, 1.999 − 2, 1.9999 − 2, 1.99999 − 2, . . .
Now name any positive number, however small. For example,
"The width of a hydrogen atom![]() " Then the absolute values of those differences (which are negative) ultimately become and remain less than that small number. The differences, in other words, between the values of x and their limit become closer and closer to 0.
" Then the absolute values of those differences (which are negative) ultimately become and remain less than that small number. The differences, in other words, between the values of x and their limit become closer and closer to 0.
When a variable x approaches a limit l, we symbolize that as x ![]() l . Read: "The values of x approach l as a limit," or simply, "x approaches l." In the example above, x
l . Read: "The values of x approach l as a limit," or simply, "x approaches l." In the example above, x ![]() 2. "x approaches 2."
2. "x approaches 2."
We also say that a sequence converges to a limit. Thus the above sequence converges to 2.
Left-hand and right-hand limits
Now the sequence we chose were values less than 2. Hence we say that x approaches 2 from the left. We write
x ![]() 2−
2−
But we can easily construct a sequence that converges to 2 from the right; that is, a sequence of values that are more than 2. For example,
2.2, 2.1, 2.01, 2.001, 2.0001, 2.00001, . . .
In this case, we write x ![]() 2+ .
2+ .
But again, no matter what small number we name, if we go far enough out in the sequence |x − 2|, the values of that difference ultimately will become less than that small number.
Again, when we say that a variable x approaches a "limit" l, we mean that the values of x get closer and closer to l. Yet the values of x are never equal to l.
We summarize this in the following definition. But first, x is not the only variable. y is a variable. And y will be a function of x -- f(x) -- which is also a variable. And when we come to the definition of the derivative, Δx or h will be the variable. In the following, then, we will use the letter z to represent any variable.
DEFINITION 2.1. The limit of a variable. We say that a variable z approaches the number l as a limit if a sequence of values of z are such that the values of the sequence |z − l| (with no term of that sequence having z equal to l) ultimately become and remain less than any positive number we might name, however small.
When that condition is satisfied, we
write z ![]() l.
l.
Thus, if Δx is the variable, and a sequence of its values approaches a limit 0, say, then we write Δx ![]() 0.
0.
The limit of a function
We have defined the limit of a variable, but what we typically have is a function of a variable -- which is also a variable. For example,
y = f(x) = x².
Now, a sequence of values of x will force a sequence of values of f(x). The question is: If the values of x approaches a limit, will the corresponding values of f(x) also approach a limit? If that is the case -- if f(x) approaches a limit L when x approaches a limit l -- then we write
![]()
"The limit of f(x) as x approaches l, is L."
In fact, let us see what happens to f(x) = x² as x ![]() 2−. Suppose again that x assumes this sequence of values:
2−. Suppose again that x assumes this sequence of values:
1.9, 1.99, 1.999, 1.9999, 1.99999, . . .
x² will then assume this sequence:
(1.9)², (1.99)²), (1.999)², (1.9999)², (1.99999)², . . .
It is easy to see that x² approaches 2² = 4.
![]()
Again, this means that if we go far enough out in the sequence of differences, x² − 4 --
(1.9)² − 4, (1.99)² − 4, (1.999)² − 4, (1.9999)² − 4, . . .
-- then the absolute values of all subsequent terms eventually will be less than any positive number we name, however small.
Moreover, if we consider a sequence x ![]() 2+:
2+:
2.2, 2.1, 2.01, 2.001, 2.0001, 2.00001, . . .
then terms of the sequence x² − 4 --
(2.2)² − 4, (2.1)² − 4, (2.01)² − 4, (2.001)² − 4, . . .
-- again will eventually be less than any small number.
4 is the limit of f(x) whether x approaches from the left or from the right. Therefore we can drop the + or − and simply write:
![]()
To summarize:
DEFINITION 2.2. The limit of a function at a point. If f is a function of x, then this notation
![]()
means:
For every sequence of values of x that approach ![]() as a limit -- whether from the left or from the right -- the corresponding values of f(x) approach L as a limit. (Definition 2.1.)
as a limit -- whether from the left or from the right -- the corresponding values of f(x) approach L as a limit. (Definition 2.1.)
In other words, for the limit of f(x) to exist at a point x = l , the left-hand and right-hand limits must be equal.
![]()
We will see that this definition of the limit existing at a point, becomes the definition of the function being continuous at that point -- if L is the value of the function at that point; that is, if L = f(![]() ). (Definition 3.1.)
). (Definition 3.1.)
The most important limit -- the limit on which calculus hinges -- is called the derivative. All the other limits studied in Calculus I are logical fun and games, never to be heard from again.
Now here is an example of a function not approaching a limit:
![]()
As x approaches 0 -- as it becomes a very small number -- its
| reciprocal | 1 x |
becomes a very large number. In fact, it will become |
larger than any number we name. It does not approach a limit.
| * | * | * |
Let us now prove that a certain limit exists, namely, the limit of f (x) = x as x approaches any value c. (That f(x) also approaches c should be obvious.)
THEOREM. If f (x) = x, then for any value c,
![]()
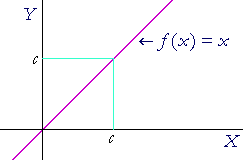
For, if a sequence of values of the variable x approaches c (Definition 2.1), then a sequence of values of the function f(x) = x will also approach c (Definition 2.2).
For example,
![]()
Theorems on limits
To help us calculate limits, it is possible to prove the following.
In other words:
The limit of a sum is equal to the sum of the limits.
The limit of a product is equal to the product of the limits.
The limit of a quotient is equal to the quotient of the limits,
provided the limit of the denominator is not 0.
In addition, if c is a constant -- that is, independent of x -- then
| 4) |
![]()
| Let x approach 4: e.g. 4 | 1 2 |
, 4 | 1 4 |
, 4 | 1 8 |
, 4 | 1 16 |
, 4 | 1 32 |
, . . . -- then the |
value of 5 -- or any constant -- does not change. It is a constant!
When c is a constant but f depends on x, then
| 5) |
A constant may pass through the limit sign. (This follows from Theorems 2 and 4.) For example,
![]()
Example 1. Quote Theorems 1) through 5) to prove the following:
![]()
| Solution. x² = x· x. And we have proved that | exists, and is |
| equal to 4. Therefore, | according to Theorem 2. |
It should be clear from this example that to evaluate the limit of any power of x, we simply evaluate the power at that value. Repeated application of Theorem 2 affirms that.
| Problem 2. |
![]()
Problem 3. Evaluate the following limits, and justify your answers by quoting Theorems 1 through 5.
![]()
43 + 4 = 64 + 4 = 68. This follows from Theorem 1 and Theorem 2.
![]()
4² + 1 = 16 + 1 = 17. This follows from Theorem 1 and Theorem 4.
![]()
5· 4² = 5· 16 = 80. This follows from Theorem 5.
| 15 5 |
= 3. |
The limits of the numerator and denominator follow from Theorems 1, 2, and 4. The limit of the fraction follows from Theorem 3.
Limits of polynomials
The student might think that to evaluate a limit all we do is evaluate the function at that point. And for the most part that is true![]() One of the most important classes of functions for which that is true are the polynomials. (Topic 6 of Precalculus.) A polynomial with argument x has this general form:
One of the most important classes of functions for which that is true are the polynomials. (Topic 6 of Precalculus.) A polynomial with argument x has this general form:
anxn + an−1xn−1 + . . . + a1x +a0
where n is a whole number, and an![]() 0.
0.
Therefore, according to the Theorems on limits, to evaluate a polynomial as the argument x approaches any value c, simply evaluate the polynomial at that value.
If P(x) is a polynomial, then
![]()
(We will see that this is equivalent to saying that polynomials are continuous functions. Definition 3.1.)
It is important to understand, however, that when we write
![]()
x is never equal to c, and P(x) is never equal to P(c)![]() Both c and P(c) are approached as limits. "Closer and closer." Nevertheless, we can evaluate the limit simply by evaluating the function at that point.
Both c and P(c) are approached as limits. "Closer and closer." Nevertheless, we can evaluate the limit simply by evaluating the function at that point.
| Problem 4. Evaluate |
5(1) − 4(−1) + 3(1) − 2(−1) + 1
= 5 + 4 + 3 + 2 + 1
= 15.
| Problem 5. Evaluate |
On replacing x with c, c + c = 2c.
| Problem 6. Evaluate |
[Hint: This is a polynomial in t.]
On replacing t with −1:
3(−1)² −5(−1) + 1 = 3 + 5 + 1 = 9
| Problem 7. Evaluate |
[Hint: This is a polynomial in h.]
On replacing h with 0, the limit is 4x³.
Some of the most important limits, however, will not be polynomials.
| They will be limits of certain quotients -- and they will appear to be | 0 0 |
! |
Making sense of that will be our challenge.
Example 2. Consider the function f(x) = x + 2, whose graph is a simple straight line. And just to be perverse (and to illustrate a logical point to which we shall return in Lesson 3), let f(x) not exist when x = 2. That is, let
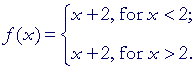
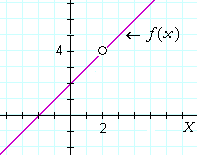
In other words, the point (2, 4) does not belong to the function; it is not on the graph.
Yet the limit as x approaches 2 -- whether from the left or from the right -- is 4![]()
![]()
For, every sequence of values of x that approaches 2 can come as close to 2 as we please. (The limit of a variable is never a member of the sequence, in any case; Definition 2.1.) Hence the corresponding values of f(x) will come closer and closer to 4. Definition 2.2 will be satsisfied.
![]()
Next Lesson: Continuous functions
www.proyectosalonhogar.com
