2
SIGNED NUMBERS
The two parts of a signed number
Subtracting a larger number from a smaller
IN ARITHMETIC, we cannot subtract a larger number from a smaller:
2 − 3
But in algebra we can. And to do it, we invent "negative" numbers.
2 − 3 = −1 ("Minus 1" or "Negative 1")
This is, since
2 − 2 = 0,
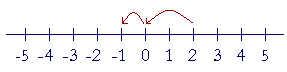
then 2 − 3 is one "less" than 0. We call it −1. −1 is a signed number.
1. What are the two parts of a signed number?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
Its algebraic sign, + or − , and its absolute value. The absolute value is simply the numerical value, that is, the number without its sign.
The algebraic sign of +3 ("plus 3" or "positive 3") is + , and its absolute value is 3.
The algebraic sign of −3 ("negative 3" or "minus 3") is − . The absolute value of −3 is also 3.
As for the algebraic sign + , normally we do not write it. The algebraic sign of 2, for example, is understood to be + .
As for 0, it is useful to say that it has both signs: −0 = +0 = 0. (See Lesson 11, Problem 11.)
When we place a number within vertical lines, |−3|, it means the absolute value of that number.
| |−3| | = | 3 |
| |3| | = | 3 |
Problem 1. Evaluate each of the following.
| a) | |6| = 6 | b) | |−6| = 6 | c) | |0| = 0 | ||
| c) | |3 − 1| = 2 | d) | |1 − 3| = 2 | ||||
2. How do we subtract a larger number from a smaller? What
5 − 8
1. will be the sign of the answer?
It would not be wrong to say that we cannot take 8 from 5. We can, however, take 5 from 8 -- and that is what we do -- but we report the answer with a minus sign.
5 − 8 = −3
Even in algebra we can only do ordinary arithmetic.
We may say that this is the first rule of signed numbers:
To subtract a larger number from a smaller,
subtract the smaller from the larger, but report
the answer as negative.
1 − 5 = −4
We actually do 5 − 1.
It was in order to subtract a larger number from a smaller that negative numbers were invented.
3. What is the only difference between 8 − 5 and 5 − 8 ?
The algebraic signs. They have the same absolute value.
Problem 2. Subtract.
| a) 3 − 5 = −2 | b) 1 − 8 = −7 | |
| c) 8 − 14 = −6 | d) 20 − 65 = −45 | |
Problem 3. You have 20 dollars in the bank and you write a check for 25 dollars. Now what is your balance?
20.00 − 25.00 = −5.00
The number line
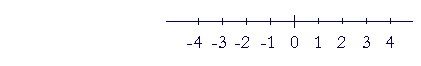
The number line is a kind of "ruler" centered on 0. The negative numbers fall to the left of 0; the positive numbers fall to the right.
We imagine every number to be on the number line. And so the fraction ½ will fall between 0 and 1; the fraction −½ is between 0 and −1; and so on.
4. What is an integer?
Any positive or negative whole number, including 0.
0, 1, −1, 2, −2, 3, −3, etc.
On the number line, we typically place the integers.
The negative of each number
Every number will have a negative. The negative of 3, for example, will be found at the same distance from 0, but on the other side.
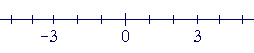
It is −3.
Now, what number is the negative of −3?
The negative of −3 will be the same distance from 0 on the other side. It is 3.
−(−3) = 3
"The negative of −3 is 3."
This will be true for any number a:
−(−a) = a
"The negative of −a is a."
What is in the box is called a formal rule . This means that whenever we see something that looks like this --
−(−a)
-- something that has that form, then we may rewrite it in this form:
a
For example,
−(−12) = 12
To learn algebra is to learn its formal rules. For, what are calculations but writing things in a different form? In arithmetic, we rewrite 1 + 1 as 2. In algebra, we rewrite −(−a) as a.
Problem 4. Evaluate the following.
a) −(−10) = 10 b) −(2 − 6) = 4 c) −(1 + 4 − 7) = 2
d) −(−x) = x
Next Lesson: Adding and subtracting signed numbers
www.proyectosalonhogar.com
