12
THE EXISTENCE
OF
IRRATIONAL NUMBERS
This continues the previous Topic.
NO ONE HAS EVER BEHELD the actual value of ![]() . Or π. Or any irrational number. All we have ever seen are rational approximations -- even to hundreds of thousands of decimal places. In what sense, then, are these irrationals numbers? Just to name something will not magically create it
. Or π. Or any irrational number. All we have ever seen are rational approximations -- even to hundreds of thousands of decimal places. In what sense, then, are these irrationals numbers? Just to name something will not magically create it![]() We certainly need irrational numbers to name ratios, yet the question of their existence is a fundamental logical problem.
We certainly need irrational numbers to name ratios, yet the question of their existence is a fundamental logical problem.
The Greeks did not admit irrational numbers. They were quite content to say that incommensurable magnitudes simply are not in the same ratio as two natural numbers. This did not prevent them from approximating ![]() , just as we must if we want to know it and use it.
, just as we must if we want to know it and use it.
Modern mathematics, on the other hand, is virtually based on the existence of irrationals. For with the symbols for the irrationals -- ![]() ,
, ![]() , and so on -- scientists can perform written calculations that previously were impossible. No man would have landed on the Moon had it not been for irrational numbers. They are the essential links between arithmetic
and geometry; between written computations and space-time. As far as the mathematics of number and magnitude is concerned, the invention of irrationals has been the main development since the 3rd century, B.C.
, and so on -- scientists can perform written calculations that previously were impossible. No man would have landed on the Moon had it not been for irrational numbers. They are the essential links between arithmetic
and geometry; between written computations and space-time. As far as the mathematics of number and magnitude is concerned, the invention of irrationals has been the main development since the 3rd century, B.C.
Knowledge of irrational numbers
Nevertheless, we must ask, In what sense is an irrational number knowable? What is our knowledge of it?
Answer. The essence of a number in general is: We know whether it is
| less than or more than another number. 8 is less than 9. | 3 4 |
is more than | 2 3 |
. |
Therefore our knowledge -- if not the very existence -- of any number must be just that. To say, then, that we know an irrational number -- that it is indeed a number -- we must be able to place it with respect to order relative to any rational number. We must be able to decide whether the irrational number is less than or greater. For, the rational numbers are what we definitely know.
Is ![]() , then, less than or greater than 1.41?
, then, less than or greater than 1.41?
We must compare them by squaring. (![]() )2 = 2. (1.41)2 = 1.9881. Therefore,
)2 = 2. (1.41)2 = 1.9881. Therefore, ![]() > 1.41.
> 1.41.
Is ![]() less than or greater than 1.42?
less than or greater than 1.42?
(1.42)2 = 2.0164. Therefore, ![]() < 1.42.
< 1.42.
We have found, then, that ![]() falls between 1.41 and 1.42 --
falls between 1.41 and 1.42 --
1.41 < ![]() < 1.42.
< 1.42.
Continuing to the third decimal place, we would find
1.414 < ![]() < 1.415.
< 1.415.
In this way, we could place ![]() with respect to order relative to any rational number. We may say then that
with respect to order relative to any rational number. We may say then that ![]() is, in fact, a number.
is, in fact, a number.
Real numbers
We have two ideas of number.
1) Number as discrete units. These are the numbers (or rather the numerals) we use for counting. These are the natural numbers.
2) Number as continuous magnitude. These are the numbers we need for measuring. These are the rationals and irrationals.
The technical term for number as magnitude is real number.
Here are 6 discrete units,
//////
which, we must be admit, is our fundamental idea of 6.

The line AB is a picture of the real number 6, in the sense that if AE is the unit, then, proportionally,
AB : AE = 6 : 1.
A real number, then, is a number required as the "address" of any
![]()
point P on the number line. A real number must name the distance of that point from 0. The real number must name the ratio of that distance to 1.
We have seen that the rational numbers are not sufficient for that task, because lengths can be incommensurable. Irrational numbers therefore were invented.
Problem 1. In terms of parts, what is the difference between the real number 10 and the natural number 10?
The real number 10 is continuous -- it could be divided into any parts. The natural number 10, on the other hand, has only half, a fifth part, and a tenth part.
Problem 2. We have classified numbers as rational, irrational, and real. Name all the categories to which each of the following belongs.
| a) 2 | Real, rational. | b) | 3 5 |
Real, rational. |
| c) 11 | 1 9 |
Real, rational. | d) |
Real, irrational. |
e) Cube root of 8 = 2. Real, rational.
f) Cube root of 9. Real, irrational.
g) 3.1415926535897932384626433
Real, rational. Any complete
g) decimal is rational. This decimal is an approximation to pi.
| h) |
i) |
j) Fourth root of 10. Real, irrational.
*
So. We can now return to the question we posed at the beginning of this inquiry:
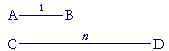
If AB, CD are lengths, will there always be a number n such that, proportionally,
AB is to CD as 1 is to n?
Can "the ratio of two lengths" (whatever that means) always be named? For, numbers have names. 1, 9.6, ![]() ,
, ![]() . But names are discrete, while lengths -- and hence their ratios -- are continuous
. But names are discrete, while lengths -- and hence their ratios -- are continuous![]()
Or are there numbers with no names? If so, then in what sense are they numbers? What is our knowledge of them? Can we place them with respect to order relative to any rational number? A continuum of lengths make sense. But does a continuum of names?
If we see the following,
![]() = 1.4142135623730950488. . . ,
= 1.4142135623730950488. . . ,
then we could make sense of it. We could identify the decimal on the right as approximating a certain real number. (See Lesson 2 of Topics in Precalculus.)
But could we make sense of it if we had only the right-hand side and not the left? Could we say that it is a number? What would be our knowledge of it? How would we calculate the next digit? What would be the name of that "number"? (And if we guessed that it might be ![]() , we would still be trying to name it
, we would still be trying to name it![]() )
)
Just as there are more realities than there are words in any dictionary, so numbers -- names -- can never exhaust the lengths of lines.
For a more detailed discussion, see the Appendix to An Approach to Calculus, What is a number?.
www.proyectosalonhogar.com
