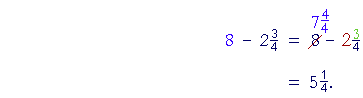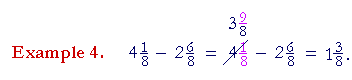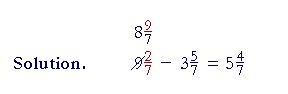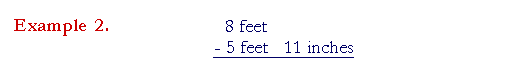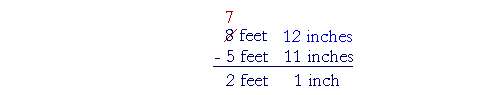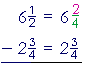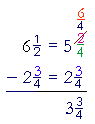To subtract 3-fourths from 8, we must make fourths. To do this,
| break off 1 from 8, and decompose it into |
4
4 |
: |
(Lesson 20, Example 4.) Therefore,
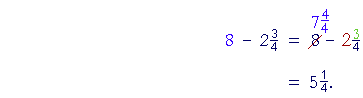
| "2 from
7 is 5. |
3
4 |
from |
4
4 |
is |
1
4 |
." |
| Example 2. |
6 − 1 |
2
3 |
= |
5 |
3
3 |
− 1 |
2
3 |
| |
| |
= |
4 |
1
3 |
. |
| "1 from 5 is 4. |
2
3 |
from |
3
3 |
is |
1
3 |
." |
Example 3. Subtracting mixed numbers. Let us now compare this problem
| with the previous one. We cannot take |
2
3 |
from |
1
3 |
. Therefore, we will again |
write
| but here we will add the |
3
3 |
to |
1
3 |
: |
| 6 |
1
3 |
= |
5 |
3
3 |
+ |
1
3 |
| |
| |
= |
5 |
4
3 |
. |
Therefore,
| 6 |
1
3 |
− 1 |
2
3 |
= 5 |
4
3 |
− 1 |
2
3 |
= 4 |
2
3 |
. |
| "1 from 5 is 4. |
2
3 |
from |
4
3 |
are |
2
3 |
." |
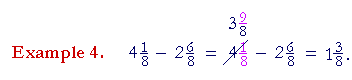
| Break off 1 from 4. Express it as |
8
8 |
, and add it to |
1
8 |
: |
| 4 |
1
8 |
= 3 |
8
8 |
+ |
1
8 |
= 3 |
9
8 |
. |
Now the mystery if any is, How does that numerator get to be 9?
9 is the sum of the original numerator 1 and denominator 8:

|
Example 5. Write the missing numerator: 9 |
2
5 |
= 8 |
?
5 |
7 is the sum of denominator plus numerator: 5 + 2.
| Example 6. 9 |
2
7 |
− 3 |
5
7 |
= ? |
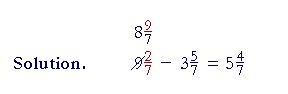
| 9 |
2
7 |
becomes 8 |
9
7 |
. The improper numerator 9 is the sum of the |
| denominator and numerator of |
2
7 |
: 7 + 2 = 9. |

Solution. First, we must make the
denominators the same:
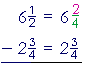
| We cannot take |
3
4 |
from |
2
4 |
; therefore, on breaking off 1 from 6, the
|
| fraction |
2
4 |
becomes 4-fourths + 2 -fourths = 6-fourths: |
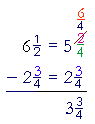
| " |
3
4 |
from |
6
4 |
is |
3
4 |
. 2 from 5 is 3." |
Please "turn" the page and do some
Problems.
or
Continue on to the next Lesson.
Previous Section
Introduction | Home | Table of Contents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com
|