|
Lesson 2 THE MEANING OF DECIMALSIn this Lesson, we will answer the following:
The counting numbers have two forms called cardinal and ordinal. |
||||||||||||||
|
||||||||||||||
|
The cardinal numbers answer the question How much? or How many?. |
||||||||||||||
|
||||||||||||||
|
The ordinal numbers answer the question Which one?. Every language has both cardinal and ordinal numbers. Parts Here are the multiples of 5: 5, 10, 15, 20, 25, 30, etc. 5 is the first multiple of 5. 10 is the second multiple; 15, the third; and so on. Now, 5 is a part of each one of its multiples (except itself). Since 15 is the third multiple of 5, we say that 5 is the third part of 15. We use that same ordinal number to name the part. 5 is the fourth part of 20, the fifth part of 25, the tenth part of 50, the hundredth part of 500. The ordinal number names which part. The decimal system Since our numbering system is based on the powers of 10, it is called a decimal system. Decem in Latin means ten. In the previous Lesson we learned about whole numbers. Here we will learn about numbers that are less than 1, that is, that are parts of 1. They are the numbers we need for measuring rather than counting. Each part of 1 will be named by an ordinal number. And since this is a decimal system, those parts will be called tenths, hundredths, thousandths, and so on. First, we will divide 1 into tenths, that is, into ten equal pieces. This is illustrated below. The rectangle representing One has been divided into Tenths.
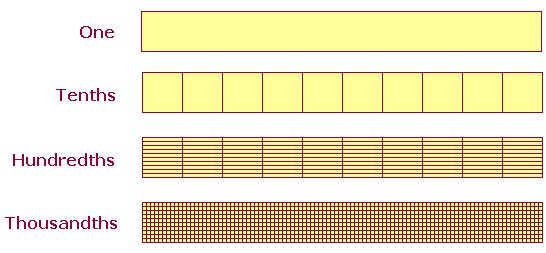
If each Tenth is divided into ten equal pieces, then each thin rectangle will be a hundredth part of One. If each Hundredth is divided into ten equal pieces, then each tiny piece will be a thousandth part of One. And so on. These are called the decimal units. |
||||||||||||||
|
||||||||||||||
|
The sequence of names of the decimal units follows the same sequence as the powers of 10. They are those powers in their ordinal form.
Let us follow the powers of 10 to the right: We arrive at the next number by taking the tenth part. The tenth part of 1000 is 100. The tenth part of 100 is 10. The tenth part of 10 is 1. And the tenth part of 1 is the first decimal unit: .1 -- "one-tenth," which we write with a decimal point. That number which we call "one-tenth" is, in fact, one tenth of 1. We will see in Lesson 19 that we write the names of the fractions hyphenated, but not the names of the parts. |
||||||||||||||
|
||||||||||||||
|
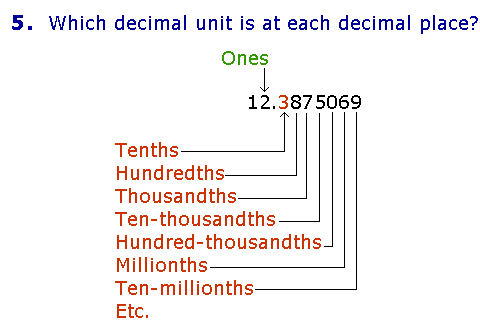
Whole units | Decimal units 412.387056 This is the whole number 412 plus a fractional part. 412.3 = 412 and (plus) 3 tenths. Any number written with a decimal point is loosely called a decimal. Specifically, a number less than 1 that is written with a decimal point is called a decimal fraction; a number written with a numerator and denominator is called a common fraction (Lesson 19). |
||||||||||||||
|
||||||||||||||
|
The first position to the right of the decimal point is called the 1st decimal place. It shows the number of Tenths. In the number above, there are 3 tenths. The 2nd decimal place shows the number of Hundredths. In that number, there are 8 hundredths. And so on. The first digit to the left of the decimal point -- the 2 -- shows the number of Ones. Thus, 12 is the whole number. The entire number has 12 whole units plus 3 tenths, plus 8 hundredths, plus 7 thousandths, and so on. Example 1. In this number 534.267 a) there are how many ones? Answer. 4. The ones place is the first digit to the left of the decimal point. b) How many hundredths? Answer. 6. Hundredths (ordinal) is a decimal unit. It falls to the right of the decimal point. c) How many hundreds? Answer. 5. Hundred (cardinal) is a whole unit. It falls to the left of the decimal point. Example 2. Expanded form. Write this number 534.267 in expanded form (Lesson 1). Answer. 534.267 = 5 Hundreds + 3 Tens+ 4 Ones + 2 Tenths + 6 Hundredths + 7 Thousandths. Or, using common fractions:
In the first decimal place, 2, notice that the denominator 10 has one 0. In the second decimal place, 6, the denominator has two 0's. In the third place, three 0's; and so on. In the sixth decimal place, the denominator would have six 0's. 1,000,000. The sixth decimal place is millionths. At this point, please "turn" the page and do some Problems. or Continue on to Section 2.
Introduction | Home | Table of Contents Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
||||||||||||||
