S k i l l
 i n
A R I T H M E T I C

Table of Contents | Home | Introduction

Lesson 6

THE MEANING OF SUBTRACTION

Mental Calculation


First, we will see the meaning of subtraction. Then we will see methods for achieving it.


In this Lesson, we will answer the following:

  1. What is the problem in subtraction?
  2. How can we find the difference between a one-digit and a two-digit number?

    Section2

  3. How can we find the difference by the ending?
  4. How can we find the difference between two-digit numbers?

    Section 3

  5. How do we complete 100?
  6. How do we find the difference by rounding off?

IN ADDITION, we are given two numbers and we have to find their sum.

28 + 7 = ?

But in what is called the inverse of addition, we are given the sum and we have to find one of the two numbers.

28 + ? = 35

That has been called "subtraction ."  It is finding the difference between two numbers.  It is finding what number we have to add.

28 + 7 = 35.

35 − 28 = 7.
 1.   What is the problem in subtraction?
 
Larger − Smaller = Difference
 
  Given two numbers, a larger and a smaller, we are to find the number we must add to the smaller number to equal the larger. That number is called their difference.

If the two numbers are equal, of course, then their difference is 0.

5 − 5 = 0.

The traditional terms subtrahend and minuend are left-overs from written calculation. The subtrahend was the number written under and taken away. The minuend was the number made less. Both refer to a written method, not to the meaning of subtraction as the inverse of addition, which is finding the number to add.

"Subtraction" itself is a historical term, meaning "taken away from below." We should try to coin a new term that emphasizes the inverse of addition.

Example 1.   How much is 149?

Answer.  9 plus what number is 14?

9 + 5 = 14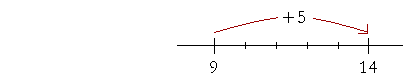

9 + 5 = 14

149 = 5

We can say that the difference of two numbers is the distance between them.  How far is it from 9 to 14?  A distance of 5.

Here is a simple example:

86 = 2  because  6 plus 2 = 8.

Knowing this, we would also know

8060  =  20   because 60 plus 20 is 80.
 
8460  =  24   because 60 plus 24 is 84.
 
812600  =  212   because 600 plus 212 is 812.

"Subtracting" is adding to the smaller number.

The complement to 10

The student should know all the ways of  "completing" 10.  For example,

103 = ?

3 plus what number makes 10?   7, of course.  7 is called the complement to 10 of 3.   7 "completes" 3 to make 10.

Example 2.   106 = 4.  In fact, whenever we take a 6 from any multiple of 10 -- 20, 30, 40, 50, 60 -- we always get a 4.

30 − 6 = 24

40 − 6 = 34

80 − 6 = 74

Similarly,

508 = 42

709 = 61

2003 = 197

$8.004¢ = $7.96 

Each difference ends in the complement to 10 of the smaller number.  These are not problems to write in a column and do some written method.

Let us now look at subtracting from a two-digit number.  We often simply count backwards.

50 − 1 = 49.

60 − 2 = 58.

70 − 3 = 67.
 2.   How can we find the difference between a one-digit and a two-digit number, mentally?
523
 
  Break off from the smaller number the ones digit
of the larger, and subtract to get a multiple of 10.
522 = 50
 
  Then subtract the rest of the smaller number.
501 = 49
 

Example 3.   Calculate mentally  835.

 Solution.   83 − 5 = 83 − 3 − 2 = 80 − 2 = 78.

Example 4.    72 − 6 = 72 − 2 − 4 = 70 − 4 = 66

At this point, please "turn" the page and do some Problems.

or

Continue on to the next Section.


Introduction | Home | Table of Contents

Please make a donation to keep TheMathPage online.
Even $1 will help.

Copyright © 2001-2007 Lawrence Spector

Questions or comments?

E-mail:  themathpage@nyc.rr.com