|
Lesson 6 THE MEANING OF SUBTRACTIONMental CalculationFirst, we will see the meaning of subtraction. Then we will see methods for achieving it. In this Lesson, we will answer the following:
IN ADDITION, we are given two numbers and we have to find their sum. 28 + 7 = ? But in what is called the inverse of addition, we are given the sum and we have to find one of the two numbers. 28 + ? = 35 That has been called "subtraction ." It is finding the difference between two numbers. It is finding what number we have to add. 28 + 7 = 35. 35 − 28 = 7. |
||||||||||||||||||||
|
||||||||||||||||||||
|
If the two numbers are equal, of course, then their difference is 0. 5 − 5 = 0. The traditional terms subtrahend and minuend are left-overs from written calculation. The subtrahend was the number written under and taken away. The minuend was the number made less. Both refer to a written method, not to the meaning of subtraction as the inverse of addition, which is finding the number to add. "Subtraction" itself is a historical term, meaning "taken away from below." We should try to coin a new term that emphasizes the inverse of addition.
Example 1. How much is 14 Answer. 9 plus what number is 14? 9 + 5 = 14 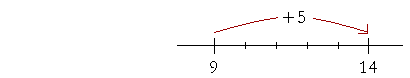
14 We can say that the difference of two numbers is the distance between them. How far is it from 9 to 14? A distance of 5. Here is a simple example: 8 Knowing this, we would also know
"Subtracting" is adding to the smaller number. The complement to 10 The student should know all the ways of "completing" 10. For example, 10 3 plus what number makes 10? 7, of course. 7 is called the complement to 10 of 3. 7 "completes" 3 to make 10.
Example 2. 10 30 − 6 = 24 40 − 6 = 34 80 − 6 = 74 Similarly, 50 70 200 $8.00 Each difference ends in the complement to 10 of the smaller number. These are not problems to write in a column and do some written method. Let us now look at subtracting from a two-digit number. We often simply count backwards. 50 − 1 = 49. 60 − 2 = 58. 70 − 3 = 67. |
||||||||||||||||||||
|
||||||||||||||||||||
|
Example 3. Calculate mentally 83 Solution. 83 − 5 = 83 − 3 − 2 = 80 − 2 = 78. Example 4. 72 − 6 = 72 − 2 − 4 = 70 − 4 = 66 At this point, please "turn" the page and do some Problems. or Continue on to the next Section. Introduction | Home | Table of Contents www.proyectosalonhogar.com |
||||||||||||||||||||
