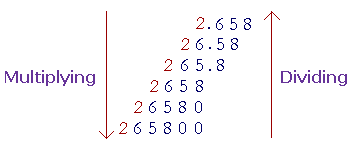MULTIPLY BY POWERS OF 10

DIVIDE BY POWERS OF 10

The Meaning of Percent

In this Lesson we will learn to multiply and divide by a power of 10 -- simply by moving the decimal point. Having done that, we can then understand scientific notation.

These are problems that do not require a calculator, and certainly should not be calculated in writing.

In this Lesson, we will answer the following:

How do we multiply a whole number by a power of 10?
How do we multiply a decimal by a power of 10?
How do we divide a decimal by a power of 10?
What do we mean by the number of decimal places?
How do we divide a whole number by a power of 10?
When is a number written in "scientific notation"?
Section 2: The Meaning of Percent
What does "percent" mean?
How can we take 1% of a number?
How can we take 10% of a number?
How do we change a percent to a number?
How do we change a number to a percent?

1.	How do we multiply a whole number by a power of 10?
36 × 10

	Add on as many 0's as appear in the power.

Examples.	36 × 10	=	360	Add on one 0.
	36 × 100	=	3600	Add on two 0's.
	36 × 1000	=	36,000	Add on three 0's.

2.	How do we multiply a decimal by a power of 10?

7.32 × 10

	Move the decimal point right as many places as there are zeros in the power.

Examples.

7.32 × 10	= 73.2	Move the decimal point one place right.
7.32 × 100	= 732	Move the point two places right: 732. However, since all the digits fall to the left of the decimal point, the answer is a whole number, 732, which we write without a decimal point.
7.32 × 1000	= 7,320	Move the point three places right. To do this, we must add on a 0. Again, the answer is a whole number.

Problem. If 5 pounds of sugar cost $2.79, how much will 50 pounds cost?

Answer. Since 50 pounds are ten times 5 pounds, they will cost ten times more. Move the decimal point one place right: $27.90. Since money has two decimal places, we add on a 0. (Lesson 3, Question 8)

3.	How do we divide a decimal by a power of 10?

63.4 ÷ 10

	Move the decimal point left as many places as there are 0's in the power. If there are not enough digits, add on 0's.

Examples.	63.4 ÷ 10	=	6.34	Move the point one place left.

	63.4 ÷ 100	=	.634	Move the point two places left.

	63.4 ÷ 1000	=	.0634	Move the point three places left. To do this, add on a 0.

Finally, we must see how to divide a whole number by a power of 10. In Lesson 1 we saw that when a whole number ends in 0's, we simply take off 0's. (Lesson 1, Question 11)

265,000 ÷ 100 = 2,650

But when a whole number does not end in 0's -- as in 265 -- then there are no 0's to chop off! We will see that we must separate digits from the right. First:

4.	What do we mean by the number of decimal places?

621.5

	They are the number of digits to the right of the decimal point.

Examples.	621.5 has one decimal place.

	6.215 has three decimal places.

	6,215 has no decimal places. It is a whole number.

5.	How do we divide a whole number by a power of 10?

265 ÷ 10

	Starting from the right of the whole number, separate as many decimal places as there are 0's in the power. If there are not enough digits, add on 0's.

Examples.	265 ÷ 10	= 26.5	Starting from the right of 265, separate one decimal place.

	265 ÷ 100	= 2.65	Separate two decimal places.

	265 ÷ 1000	= .265	Separate three decimal places.

Again, as in Lesson 1, consider this array:

Place values

As we move down the list -- as we push the digits one place left -- the number has been multiplied by 10, because the next place is worth 10 times more. (As we move from 2.658 to 26.58, we go from 2 ones to 2 tens.) It appears, though, as if the decimal point has shifted one place right, or, with whole numbers, that a 0 has been added on.

As we move up the list -- as we push the digits to the right -- each number has been divided by 10.

And so we can easily multiply or divide by a power of 10 because of the written system itself. Each place belongs to the next power of 10.

6.	When is a number written in "scientific notation"?

	A number is written in scientific notation when there is one non-zero digit to the left of the decimal point.

2.345

That number is written in scientific notation. There is one digit to the left of the decimal point -- 2 -- and it is not 0.

In general, a number written in scientific notation will be multiplied by 10 raised to an "exponent."

2.345 × 10³ 2.345 × 10⁻³

Without going into the details of what the exponents 3 and −3 actually mean, we can state the following :

A positive exponent means to multiply by a power of 10. A negative exponent means to divide.

Briefly, the exponent indicates the number of 0's
in the power of 10. To go further into the meaning of an exponent, see Lessons 13 and 21 of Skill in Algebra.

Therefore, if a number is written in scientific notation, then to express it as a standard number, we can state the following rule:

If the exponent is positive, move the decimal point right as many places as indicated by the exponent.

If the exponent is negative, move the decimal point left as many places as indicated by the exponent.

Example 1. Each number is written in scientific notation. What number is it?

a) 5.42 × 10³ = 5,420. Move the decimal point three places right.

b) 5.42 × 10⁻³ = .00542 Move the decimal point three places left.

Example 2. Write each number in scientific notation.

a)	123.4 = 1.234 × 10²

	The scientific notation begins 1.234. To get back to 123.4, we have to move the point 2 places right. We have to multiply by 10 with exponent +2.

b)	380,000 = 3.8 × 10⁵

	The scientific notation begins 3.8. To get back to 380,000, we have to move the point 5 places right. We have to multiply by 10 with exponent +5.

c)	.0012 = 1.2 × 10⁻³

	The scientific notation begins 1.2. To get back to .0012, we have to move the point 3 places left. We have to multiply by 10 with exponent −3.

At this point, please "turn" the page and do some Problems.

Continue on to the next Section.

Introduction | Home | Table of Contents