Triángulos
Fecha de primera versión: 28-03-98
Fecha de última actualización: 19/04/2010
![]()
Triángulo:
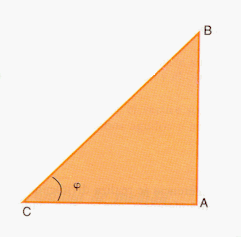 Es
un polígono que tiene tres lados y tres ángulos.
Es
un polígono que tiene tres lados y tres ángulos.
El punto donde se unen dos lados se llama vértice.
La suma de dos lados de un triángulo siempre es mayor que el tercero.
La suma de los ángulos de un triángulo es 180º.
Es muy frecuente clasificar los triángulos por los lados (equilátero, si tiene los tres lados iguales, isósceles, dos lados iguales y escaleno, ningún lado igual) y por los ángulos (rectángulo si tiene un ángulo de 90º, acutángulo si todos los ángulos son menores de 90º y obtusángulo si tiene un ángulo mayor de 90º).
El nombre de isósceles, viene de iso, igual, y de skelos, piernas. Triángulo isósceles, significaría triángulo con dos piernas iguales. Triángulo escaleno, significaría triángulo cojo.
El triángulo más famoso es el triángulo rectángulo. El lado mayor de un triángulo rectángulo se llama hipotenusa y los pequeños, catetos. Este triángulo tiene una propiedad muy importante: Si construimos unos cuadrados en sus lados, la suma del área de los cuadrados construidos en los catetos es igual al área del cuadrado construido en la hipotenusa (escrito de forma matemática: a2 + b2 = c2).
Un triángulo isósceles en el que el cociente entre uno de sus lados y el lado menor sea el número de oro se llama triángulo áureo. Los ángulos de la base del triángulo áureo miden 72º y el del vértice 36º.
Mediana
Es la recta que pasa por un vértice y por el punto medio del lado opuesto. Hay tres medianas y las tres se cortan en un punto que se llama centro de gravedad (o baricentro) del triangulo. Arquímedes estudió el baricentro en su libro Sobre el equilibrio de los planos.
Si conocemos las coordenadas de los tres vértices del triángulo, el cálculo del baricentro es muy sencillo. Sean (x1, y1, z1), (x2, y2, z2), (x3, y3, z3), las coordenadas del baricentro serán:
x = (x1 + x2 + x3) / 3
y = (y1 + y2 + y3) / 3
z = (z1 + z2 + z3) / 3
La fórmula es para un triángulo en el espacio, pero se puede aplicar para un triangulo en el plano, haciendo z1 = z2 = z3 = 0 (o cualquier otro número).
Bisectriz
Es la recta que que divide el ángulo en dos partes iguales. Hay tres bisectrices y se cortan en un punto llamado incentro. Este punto tiene la particularidad de que haciendo centro en él, podemos dibujar una circunferencia interior al triángulo y que es tangente a los tres lados del triangulo. Euclides estudió el incentro en el Libro IV de los Elementos. Si unimos el incentro con los vértices del triangulo, obtenemos tres triángulos. El área del triangulo original será igual a la suma de las áreas de los tres triángulos. Es fácil demostrar que el área del triángulo es A = r.p. siendo r el radio de la circunferencia inscrita y p el semiperímetro del triángulo.
Mediatriz
Es la recta perpendicular en el punto medio de un segmento. Las mediatrices de los lados de un triángulo se cortan en un punto llamado circuncentro. Haciendo centro en este punto, podemos trazar una circunferencia que pasa por los tres vértices del triángulo. Euclides estudió el circuncentro en el Libro IV de los Elementos.
Altura
Es la recta que pasa por un vértice y es perpendicular al lado opuesto. Hay tres alturas y se cortan en un punto llamado ortocentro.
Superficie de un triángulo:
La fórmula que todos sabemos de la superficie de un triángulo es S = (b.h)/2
Hay otra fórmula menos conocida, la fórmula de Herón:
siendo p = (a + b + c)/2
Esta es la demostración de la fórmula de Herón:
Dibuja un triangulo cualquiera. Nombra los ángulos con las letras A, B y
C y los lados
opuestos a dichos ángulos como a, b y c.
Area = (b.c. sen A) / 2
a2 = b2 +c2 - 2.b.c.cos
A
Despejando cos A e igualando con la formula del seno mitad
1 - 2.sen2 A/2 = (b2 + c2
- a2) / 2bc
Desarrollando esto queda:
2.sen2 A/2 = ((a + b -c)(a - b + c)) /
2bc
llamando 2p = a + b + c
2(p-a) = b + c - a
2(p-b) = a - b + c
2(p-c) = a + b - c