Adding algebraic fractions: Level 2
Problem 7.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| a) | 1 x |
+ | 2 3x |
= | 3 + 2 3x |
= | 5 3x |
b) | 3 2x |
− | 4 2x² |
= | 3x − 4 2x² |
| c) | 1 (x + 1)² |
+ | 2 (x + 1) |
= | 1 + 2(x + 1) (x + 1)² |
= | 1 + 2x + 2 (x + 1)² |
= | 2x + 3 (x + 1)² |
| d) | 6 x(x − 1) |
+ | 2 x(x − 2) |
= | 6(x − 2) + 2(x − 1) x(x − 1)(x − 2) |
| = | 6x − 12 + 2x − 2 x(x − 1)(x − 2) |
||||
| = | _8x − 14_ x(x − 1)(x − 2) |
||||
| Example 7. Add | 4 x² − 25 |
− | 3 x² − 6x + 5 |
Note that we tend to say "add" in algebra, even though the operation is subtraction.
Solution. To construct the LCM of the denominators, we must first factor the denominators.
| 4 x ² − 25 |
− | 3 x² − 6x + 5 |
= | _4_ (x + 5)(x − 5) |
− | _3_ (x − 5)(x − 1) |
| = | 4(x − 1) − 3(x + 5) (x + 5)(x − 5)(x − 1) |
|||||
| = | _4x − 4 − 3x − 15_ (x + 5)(x − 5)(x − 1) |
|||||
| = | __x − 19__ (x + 5)(x − 5)(x − 1) |
|||||
Problem 8. Add. First factor each denominator.
| a) | x 2 |
+ | _5_ 2x + 2 |
= | x 2 |
+ | _5_ 2(x + 1) |
| = | x(x + 1) + 5 2(x + 1) |
||||||
| = | x² + x + 5 2(x + 1) |
||||||
| b) | 1 x² − x |
+ | 2 x |
= | _1_ x(x − 1) |
+ | 2 x |
| = | 1 + 2(x − 1) x(x − 1) |
||||||
| = | 1 + 2x − 2 x(x − 1) |
||||||
| = | 2x − 1 x(x − 1) |
||||||
| c) | 2 x + 3 |
+ | 12 x² − 9 |
= | 2 x + 3 |
+ | __12__ (x + 3)(x − 3) |
| = | 2(x − 3) + 12 (x + 3)(x − 3) |
||||||
| = | 2x − 6 + 12 (x + 3)(x − 3) |
||||||
| = | ___2x + 6___ (x + 3)(x − 3) |
||||||
| = | __ 2(x + 3) __ (x + 3)(x − 3) |
||||||
| = | _2_ x − 3 |
||||||
| d) | ___6___ x² + 5x + 6 |
+ | ___2___ x² − x − 6 |
= | ___6___ (x + 2)(x + 3 ) |
+ | ___ 2___ (x + 2)(x − 3) |
| = | 6(x − 3) + 2(x + 3) (x + 2)(x + 3)(x − 3) |
||||||
| = | _ 6x − 18 + 2x + 6 _ (x + 2)(x + 3)(x − 3) |
||||||
| = | _____8x − 12_____ (x + 2)(x + 3)(x − 3) | ||||||
| = | ___ 4(2x − 3) ___ (x + 2)(x + 3)(x − 3) | ||||||
Factor the numerator to see if anything might cancel.
| e) | ___3___ x² − 7x + 10 |
− | __2__ x² − 25 |
= | ___3___ (x − 2)(x − 5) |
− | ___ 2___ (x + 5)(x − 5) |
| = | 3(x + 5) − 2(x − 2) (x − 2)(x − 5)(x + 5) |
||||||
| = | _ 3x + 15 − 2x + 4 _ (x − 2)(x − 5)(x + 5) |
||||||
| = | ___ __x + 19__ ___ (x − 2)(x − 5)(x + 5) |
||||||
| f) | ___7___ 3x² − 5x + 2 |
− | ___4___ 3x² + x − 2 |
= | ___7___ (3x − 2)(x − 1) |
− | ___ 4___ (3x − 2)(x + 1) |
| = | 7(x + 1) − 4(x − 1) (3x − 2)(x − 1)(x + 1) |
||||||
| = | _ 7x + 7 − 4x + 4_ (3x − 2)(x − 1)(x + 1) |
||||||
| = | ___ __3x + 11__ ___ (3x − 2)(x − 1)(x + 1) |
||||||
Example 8. Symmetrically, we can rewrite a fraction as a sum of fractions:
| a + b + c d |
= | a d |
+ | b d |
+ | c d |
Problem 9. Rewrite each of the following as a sum of fractions, and simplify.
| a) | 1 + 2 + 3 6 |
= | 1 6 |
+ | 2 6 |
+ | 3 6 |
= | 1 6 |
+ | 1 3 |
+ | 1 2 |
| b) | 2n² − 4n + 1 n² |
= | 2n² n² |
− | 4n n² |
+ | 1 n² |
= | 2 | − | 4 n |
+ | 1 n² |
| c) | x³ + 4x² + 2 2x5 |
= | x³ 2x5 |
+ | 4x² 2x5 |
+ | 2 2x5 |
= | 1 2x² |
+ | 2 x3 |
+ | 1 x5 |
| d) | x − 1 x + 1 |
= | x x + 1 |
− | 1 x + 1 |
| Example 9. Simplify | 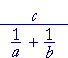 |
| Solution. | 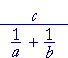 |
= | 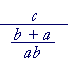 |
|||
| = | c· | ab b + a |
(Definition of division) | |||
| = | cab b + a |
or | abc a + b |
|||
Problem 10. Simplify.
| a) | 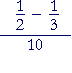 |
= | 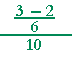 |
= | 1 6 |
· | 1 10 |
= | 1 60 |
| b) | 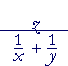 |
= | 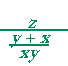 |
= z· | xy y + x |
= | zxy y + x |
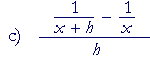 |
= | x − (x + h) (x + h)x |
· | 1 h |
|
| = | x − x − h (x + h)x |
· | 1 h |
||
| = | −h (x + h)x |
· | 1 h |
||
| = | − | 1 (x + h)x |
|||
| d) | 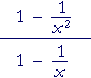 |
= | 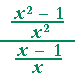 |
= | (x + 1)(x − 1) x² |
· | x x − 1 |
= | x + 1 x |
Or, on recognizing the numerator as the Difference of Two Squares:
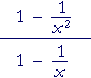 |
= | 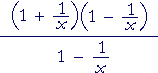 |
= 1 + | 1 x |
= | x + 1 x |
| e) | 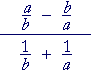 |
= | 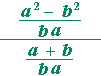 |
||
| = | (a + b)(a − b) ba |
· | ba a + b |
||
| = | a − b | ||||
Next Lesson: Equations with fractions
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com