14
DERIVATIVES OF EXPONENTIAL
AND
LOGARITHMIC FUNCTIONS
The derivative of e with a variable exponent
The system of natural logarithms
The derivative of the natural logarithm of function
The constant of proportionality
THERE ARE MANY WAYS to introduce the exponential and logarithmic functions and to find their derivatives. To begin, some definition will be required. Often it is of the number called e:
![]()
Others begin by defining the "natural logarithm," ln x, as the function
| whose derivative is | 1 x |
. Logically, we must accept the definition given. |
Analytically, though, we want the definition to be justified. (Why, for example,
| does the function whose derivative is | 1 x |
have the properties of a logarithm?) |
The definition we begin with will answer this question: "What will be the most convenient number to serve as the theoretical base for a system of logarithms?" (It will not be 10.) And we will define that number -- simply called e, for the moment -- as having the property that the derivative of ex is equal to itself.
| d dx |
ex | = ex |
To justify that implicit definition of e, we will examine the properties of an exponential function. An exponential function then implies its inverse: a logarithmic function (Topic 21 of Precalculus).
Exponential functions
An exponential function has the form y = ax, where a, the base, is a positive number typically greater than 1. Exponential functions are continuous and defined for all values of x.
Exponential functions exhibit the property of exponential growth. For we say that a quantity grows "exponentially" when it grows at a rate that is proportional to its size. That is, the bigger it is at any given time, the faster it's growing at that time. A standard example is population. The more individuals there are, the more births there will be, and hence the greater the rate of change of the population -- the number of births per year.
As another example, consider this salary offer: You are going to be hired for 30 days starting tomorrow, and you are offered two options: 1) $1,000,000 at the end of the 30 days, or 2) 1 cent now (day 0), and when you start tomorrow (day 1), your pay will double each day. That is, on the first day you will get 2 cents; on the second day, 4 cents; and so on.
Which option will you take?
If you know anything about the powers of 2 -- which grow exponentially -- you will quickly take the second option. Here, in fact, is a table of your daily pay:
| Day | Pay | |
|---|---|---|
| 10 | .01 | |
| 11 | .02 | |
| 12 | .04 | |
| 13 | .08 | |
| 14 | .16 | |
| 15 | .32 | |
| 16 | .64 | |
| 17 | 1.28 | |
| 18 | 2.56 | |
| 19 | 5.12 | |
| 10 | 10.24 | |
| 11 | 20.48 | |
| 12 | 40.96 | |
| 13 | 81.92 | |
| 14 | 163.84 | |
| 15 | 327.68 | |
| 16 | 655.36 | |
| 17 | 1,310.72 | |
| 18 | 2,621.44 | |
| 19 | 5,242.88 | |
| 20 | 10,485.76 | |
| 21 | 20,971.52 | |
| 22 | 41,943.04 | |
| 23 | 83,886.08 | |
| 24 | 167,772.16 | |
| 25 | 335,544.32 | |
| 26 | 671,088.64 | |
| 27 | 1,342,177.28 | |
| 28 | 2,684,354.56 | |
| 29 | 5,368,709.12 | |
| 30 | 10,737,418.24 |
Such are the rewards of patience. This is exponential growth. Your pay grows at a rate -- the number of dollars per day -- that is proportional to the pay itself that day.
Thus on day 0, you're paid 1 cent. Therefore the rate at which you're paid that day is 1 cent per day (almost) -- so that the next day you earn 2 cents. But on day 29 you're paid $5,368,709.12. Therefore the rate at which you're paid on that day is $5,368,709.12 per day (almost) -- so that the next day you earn $10,737,418.24![]()
The exponential function here was y = .01 × 2x. The values of x were the integers 0, 1, 2, 3, etc.
(As for why "almost" each time, the derivative of 2x is not exactly 2x. See Example 6.)
Now, to say that the rate of growth is proportional to its size, is to say that
| the derivative of ax is proportional to ax. |
| d dx |
ax | = kAx | , |
where k is the constant of proportionality. (Lesson 39 of Algebra. When we calculate the derivative below, we will see how that constant emerges naturally.)
If we now choose as base that number such that k will be 1, then that will be the most convenient base. For when we do that, the derivative will be equal to the function itself.
We show below that it is possible to choose k = 1. And when we do that, we call the base e.
| d dx |
ex | = ex |
"The derivative of ex with respect to x
is equal to ex."
It is possible to evaluate this base e, and we do that in the following Lesson. Yet its significance lies in the fact that we have chosen e so that the derivative of ex is itself. e is therefore the base of what is called the system of natural logarithms.
The derivative of e with a variable exponent
| When y = eu(x), then according to the | chain rule: |
![]()
That is,
![]()
"The derivative of e with a variable exponent
is equal to e with that exponent
times the derivative of that exponent."
Example 1. Calculate the derivative of e2x + 3.
| Solution. |
Problem 1. Calculate the derivative of ex².
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
ex²· 2x = 2x ex²
Problem 2. Calculate the derivative of the following.
a) esin x. esin x cos x
b) e−x. e−x (−1) = −e−x
c) x²ex. According to the product rule: x²ex + 2x ex
| e) | According to the quotient rule: |
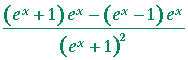 |
= | 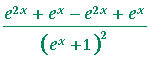 |
= | 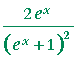 |
The system of natural logarithms
An exponential function has as its inverse a logarithmic function. (Topic 21 of Precalculus.) e is the base of the system of "natural logarithms."
We denote the logarithmic function with base e as ln x.
ln x = logex
y = ln x implies ey = x.
Here are the inverse relations:
ln ex = x and eln x = x.
And the logarithm of the base itself is always 1:
ln e = 1.
(Topic 20 of Precalculus.)
The function y = ln x is continuous and defined for all positive values of x. It will obey the usual laws of logarithms:
1. ln ab = ln a + ln b.
| 2. ln | a b |
= ln a − ln b. |
3. ln an = n ln a.
(Topic 20 of Precalculus.)
The derivative of ln x
We will now prove:
| d dx |
ln x | = | 1 x |
For, since
eln x = x,
then on taking the derivative of both sides:
![]()
| Therefore the derivative of | eln x according to the chain rule must also |
equal 1:
| = | eln x· | ||
| = | |||
This implies
| d dx |
ln x | = | 1 x |
. |
Which is what we wanted to prove.
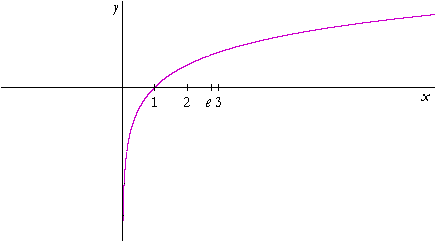
This is the graph of y = ln x. (Topic 21 of Precalculus.) The slope of the tangent line at each point is the reciprocal of x. Thus the smaller the value of x -- the closer it is to 0 -- the greater the rate of change at that point. In other words, the closer an interval is to 0, the more spread out are the values of ln x. For large values of x, on the other hand, the smaller the rate of change. In any interval far from 0, the values of ln x are clustered.
The derivative of the natural logarithm of a function
When y = ln u(x), then according to the chain rule:
![]()
That is,
![]()
| Example 2. |
| Example 3. | d dx |
ln sin x | = | 1 sin x |
· cos x | = | cos x sin x |
= cot x. |
Example 4. Find the derivative of ln x².
Solution. We may apply the laws of logarithms:
| d dx |
ln x² | = | d dx |
2 ln x, 3rd law, | |||
| = | 2 | d dx |
ln x | ||||
| = | 2 x |
. | |||||
| Example 5. Find the derivative of ln | x 3x − 4 |
. |
Solution. According to the 2nd Law:
| d dx |
ln | x 3x − 4 |
= | d dx |
[ln x − ln (3x − 4)] |
| = | |||||
| = | 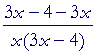 |
||||
| = | 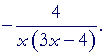 |
||||
Problem 3. Differentiate the following.
| a) ln x3. | d dx |
ln x3 = | d dx |
3 ln x | = | 3 x |
| b) (ln x)3. | 3(ln x)²· | 1 x |
= | 3(ln x)² x |
| c) ln (3x² − 4x). | 1 3x² − 4x |
· (6x − 4) | = | 6x − 4 3x² − 4x |
| d) ln (3x − 4)². | 1 (3x − 4)² |
· 2(3x − 4)· 3 | = | 6(3x − 4) (3x − 4)² |
= | 6 3x − 4 |
| e) ln cos x. | 1 cos x |
(−sin x) | = | − | sin x cos x |
= | −tan x |
| Problem 4. Calculate the derivative of ln | 2 x |
. |
| d dx |
ln | 2 x |
= | d dx |
(ln 2 − ln x) = 0 − | 1 x |
= − | 1 x |
The general power rule
We can now prove that for any exponent n:
| d dx |
xn | = nxn−1 |
Let
| y | = | xn. | ||
| Then | ||||
| ln y | = | n ln x (3rd Law). | ||
| Therefore, on taking the derivative with respect to x: | ||||
| = | n x |
|||
| so that | ||||
| y' | = | n x |
· y | |
| = | n x |
· xn | ||
| = | nxn−1. | |||
This is what we wanted to prove.
| Problem 5. Calculate the derivative of |
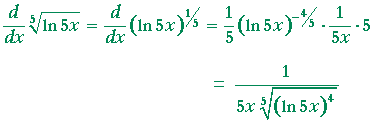
The derivative of ax
We will prove:
| d dx |
ax | = ln a· ax |
"The derivative of an exponential function with base a
is equal to the natural logarithm of the base
times the exponential function."
Let
| y | = | ax. | ||
| Then on taking the natural logarithm of both sides: | ||||
| ln y | = | x ln a. (3rd Law) | ||
| Therefore, | ||||
| = | ||||
| But by the chain rule: | ||||
| = | 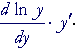 |
|||
| Therefore, | ||||
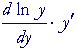 |
= | ln a | ||
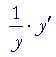 |
= | ln a | ||
| y' | = | ln a· y | ||
| That is, | ||||
| = | ln a· ax. | |||
This is what we wanted to prove.
| Example 6. | d dx |
2x | = ln 2· 2x. |
Problem 6. Calculate the derivative of y = 105x.
By the chain rule:
![]()
The constant of proportionality
| We will now calculate the derivative of y = ax by applying the definition, and |
we will see how the constant of proportionality comes about.
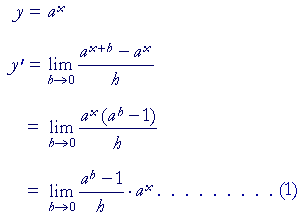
That limit is the constant of proportionality. We will therefore define the base of our logarithms to be that number a such that that limit will be 1.
To see that there is such a number a, consider these graphs:
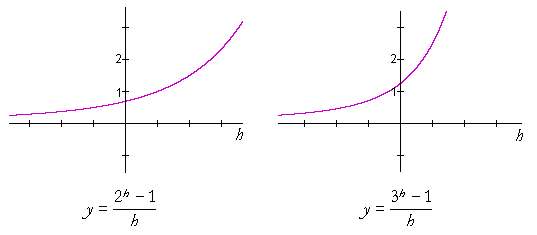
On the left, a = 2, and on the right, a = 3. (h = 0 is a removable discontinuity, for the vertical line h = 0 is not an asymptote to the graph.)
Clearly, there will be a value of a greater than 2 on the left, and less then 3 on the right, such that the graph passes exactly through y = 1.
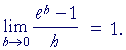
That will be the number we call e.
(In the next Lesson, we will see that e is approximately 2.718.)
Upon replacing a with e in Line (1):
| y' | = | 1· ex | = | ex. |
![]()
www.proyectosalonhogar.com
