5
THE DERIVATIVE
The rate of change of a function
at a specific point
The slope of a tangent line to a curve
The definition of the derivative
The derivative of f(x) = 2x − 5
Now the slope of a straight line indicates a constant rate of change as
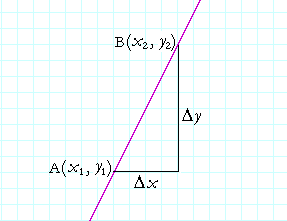
as we move from a point A on the line to a point B; so many units of y for each unit of x. (Topic 8 of Precalculus.) The slope is the number
| Δy Δx |
= | = | Change in y-coordinate Change in x-coordinate |
. |
This rate of change is constant. A straight line has one and only one slope.
If x represents time, for example, and y represents distance, then a
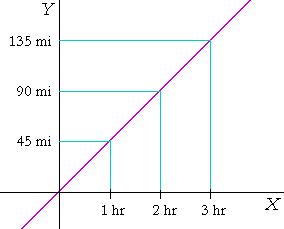
straight line graph that relates them indicates constant speed. 45 miles per hour, say -- at every moment of time.
The slope of a tangent line to a curve
Calculus however is concerned with rates of change that are not constant.
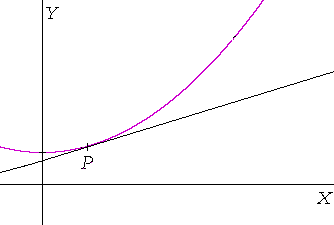
If this curve represents distance versus time, then the rate of change — the speed — at each moment of time is not constant. The question that calculus asks is: "What is the rate of change at exactly the point P ?" The answer will be the slope of a tangent line to the curve at precisely that point. And the method for finding that slope — that number — was the remarkable discovery by both Isaac Newton (1642-1727) and Gottfried Leibniz (1646-1716). That method is the fundamental procedure of differential calculus.
A secant to a curve
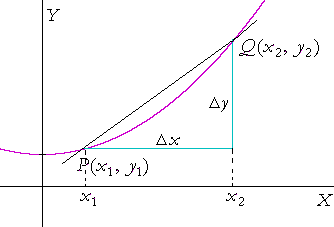
A secant is a straight line that cuts a curve. (A tangent is a straight line that just touches a curve.) Hence, consider a secant line that cuts the curve at points P and Q. The slope of the secant is the average rate of change between those two points. For example, if
![]()
then between x1 and x2 that function is changing an average of 4 units of y for every 5 units of x. But once again, the question calculus will ask is: How is the function changing precisely at x1?
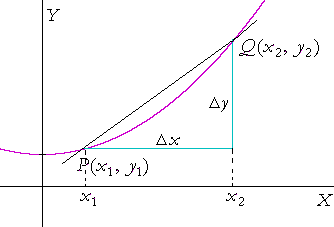
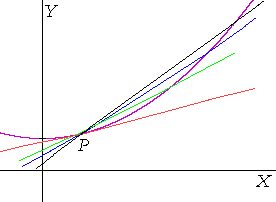
To answer, let the point Q approach the point P, and let us calculate the average rate of change as x2 gets closer and closer and closer to x1. That is, let x2 approach x1 as a limit (Lesson 2). In other words, let Δx approach 0.
We will have a sequence of secant lines each with its own slope. And the limit of that sequence will be the slope m of the tangent line
at P ![]()
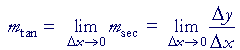
The secant will revolve about the fixed point P, and the limit of its revolving is the tangent line. The slope of the tangent will be the value of the "derivative" at that point.
The slope at a specific point
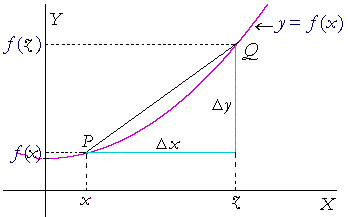
Let y = f(x). Let x be a specific point in the domain of f, and let z be another point. Then the coordinates of P are (x, f (x)), and the coordinates of Q are (z , f (z)). (Topic 4 of Precalculus.)
Therefore, the slope of the secant line PQ is
![]()
Let Δx approach 0 -- that is, let z approach x. Then the slope of the tangent line at P is
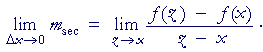
To be explicit, let us evaluate that limit for the function f(x) = x².
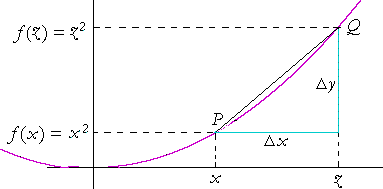
Then the coordinates of P are (x, x²), and the coordinates of Q are (z , z²).
First, we will evaluate the slope of the secant line PQ:
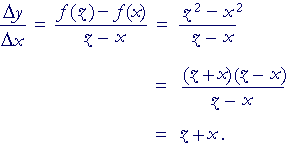
We first factored the difference of two squares (Lesson 19 of Algebra).
We then divided the numerator by z − x. (We may do that because z is never equal to x; that is, the denominator is never 0, even when we take the limit; Lesson 2).
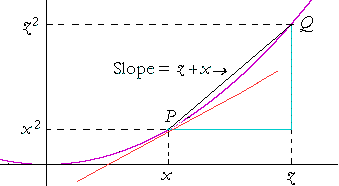
We found the slope of the secant PQ to be z + x . To find the slope of the tangent at P, we will take the limit as z approaches x.
![]()
But z + x is a polynomial in z (Lesson 2). Therefore we may evaluate that limit simply by replacing z with x.
![]()
The slope, then, of the tangent to y = x² at the point x -- the rate of change of the function at that point -- is 2x. At x = 4, for example, the slope is 2· 4 = 8. At x = −5, the slope is 2· −5 = −10. And so on.
The value of the slope is itself a function of x. In this case it is 2x. 2x is the rate of change of f(x) = x² at the specific point x.
Now, since 2x was derived from f(x) = x², 2x is called the derived function, or the derivative, of x². To remind us that it came from f(x), we write f '(x) -- "f-prime of x."
| f(x) | = | x² |
| f '(x) | = | 2x |
The definition of the derivative
Let us start again and define the slope of the tangent to a curve as a function of x.
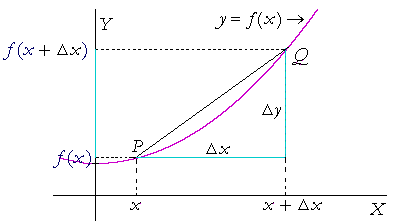
Let y = f(x), and let the coordinates of a point P on the graph be
(x, f(x)).
Let Δx be a change in the value of x, so that (x + Δx, f(x + Δx)) are the coordinates of Q.
Then
![]()
Therefore the slope of the tangent line at P -- the function we are calling f ' (x), the derivative of f(x) -- is the following limit:
This quotient --
![]()
-- is called the Newton quotient, or the difference quotient. Calculating and simplifying it is a fundamental task in differential calculus.
To simplify our calculations, then, instead of having to write Δx, we will write h.
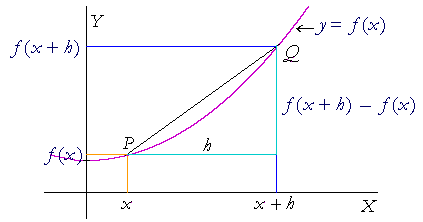
| Δx | = | h |
| Δy | = | f (x + h) − f (x) |
The difference quotient then becomes
![]()
We will therefore express the definition of the derivative as follows.
Note: On taking the limit, the difference quotient is a function of h. x is constant. It is the specific point at which we calculate the rate of change of f(x).
In practice, we must simplify the difference quotient before taking the limit. We must express the numerator --
f (x + h) − f (x)
-- in such a way that we can divide it by h.
As an example, we will apply the definition to prove the following:
| THEOREM. | f(x) | = | x² |
| implies | |||
| f '(x) | = | 2x. | |
Proof. Here is the difference quotient, which we will proceed to simplfy:
| 1) | (x + h)² − x² h |
|
| 2) | = | x² + 2xh + h² − x² h |
| 3) | = | 2xh + h² h |
| 4) | = | 2x + h. |
In going from line 1) to line 2), we squared the binomial x + h.
In going to line 3), we subtracted the x²s. That is, we subtracted f(x).
In going to line 4), we divided the numerator by h. (Lesson 20 of Algebra.)
We can do that because h is never equal to 0, even when we take the limit (Lesson 2).
We now complete the defintion of the derivative and take the limit:
| f '(x) | = | (2x + h) | |
| = | 2x. | ||
This is what we wanted to prove.
Whenever we apply the definition, we must express the difference quotient in such a way that we can evaluate the limit simply by replacing h with 0. For, that difference quotient -- in this case, 2x + h -- will be a continuous function of h.
Differentiable at a point
According to the definition, a function will be differentiable at a point if a certain limit exists there. Graphically, this means that the graph at that point will have a tangent line. At which points, then, would a function not be differentiable?
Where it does not have a tangent line![]()
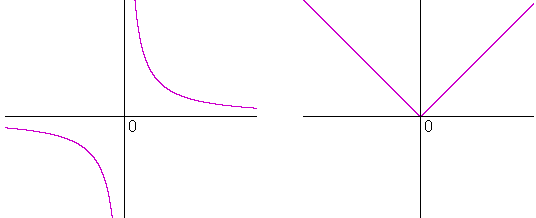
Above are two examples. The function on the left does not have a derivative at x = 0, because the function is discontinuous there. At x = 0 there is obviously no tangent.
As for the function on the right, although it is continuous at x = 0, it is not differentiable. At an acute angular point, there is no tangent.
Thus, continuity is no guarantee of differentiability.
(Conversly, though, if a function is differentiable at a point -- if there is a tangent -- it will also be continuous there. The graph will be smooth and have no break.)
The graph on the right is the absolute value function. (Topic 5 of Precalculus.) Approaching 0 from the left, the slope of the tangent line -- which is the graph itself -- is −1. The slope approaching from the right, however, is +1. The limit at 0 -- which would be the derivative -- therefore does not exist . (Definition 2.2.)
Since differential calculus is the study of derivatives, it is fundamentally concerned with functions that are differentiable at all points of their domains. Such functions are called differentiable functions.
Can you name an elementary class of differentiable functions?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Think about this yourself first!
Polynomials.
Notations for the derivative
| Since the derivative is this limit: | then a symbol for the |
| derivative is |
![]()
For example, if
| y | = | x², | |
| then, as we have seen, | |||
| = | 2x. | ||
"The derivative of y with respect to x is 2x."
We also write
y ' = 2x.
"y-prime is equal to 2x."
| This symbol by itself: | d dx |
, is called the differentiating operator. We are |
to take the derivative of what follows it. For example,
| d dx |
f(x) indicates the derivative with respect to x of f(x). |
| d dx |
(4x3 − 5) indicates the derivative with respect to x of (4x3 − 5). |
And so on.
A simple difference quotient
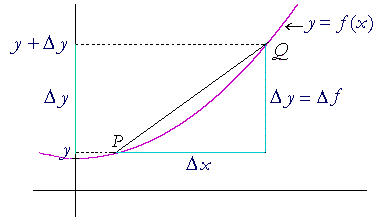
| The difference quotient is a version of | Δy Δx |
. And at times we |
will use that simple version. That is, the change in the value of a function y = f(x) is y + Δy. Hence the difference quotient is
![]()
At times it will be convenient to express the difference quotient as
![]()
Note: As Δx approaches 0 -- as the point Q moves closer to P along the curve -- then Δy, or equivalently, Δf also approaches 0. That is,
![]()
The student should now do Problems that require the definition of the derivative.
![]()
www.proyectosalonhogar.com
