Appendix
WHAT IS A NUMBER?
The existence of real numbers
Irrational numbers and their order
ARITHMETIC, IF IT IS ANYTHING, is knowledge of numbers. When confronted with geometry, arithmetic must come up with the name of a number as the measure of some magnitude, relative to a unit of measure. 5½ feet, 6.78905 meters, ![]() seconds.
seconds.
To assume that there always is such a number will miss the problem. For magnitudes are continuous. And if there is to be a number to measure every magnitude -- every length, say -- then numbers themselves must constitute a continuum. But will that be possible? And if it is, then what will be our knowledge of such numbers? The issue is as ancient as Pythagoras.
To begin our inquiry, let us ask, What is a number? And what does it mean to say that a number exists?
The natural numbers
Arithmetic begins with naming the sequence of numbers. Otherwise, we cannot count. We name the first number (which in English we call "one" ), the second ("two"), the third ("three"), and so on. Ordinality -- first, second, third -- is fundamental.
These are the names of the natural numbers, both their cardinal and ordinal forms. Having named those numbers, we can then make true statements about them, such as "Two plus two is four."
Every thing that exists, and has a name, and we can therefore call one, is a unit. One apple, one orange, one axiom. We count units, which is to say, we match them with the sequence of number-names: One apple, two apples, three apples. The natural number itself is the actual collection of
![]()
discrete units. 5 people, 10 pencils, 20 million stars. The symbols '5,' '10,' '20' -- which are called numerals -- refer to those collections of units, those numbers. That is the nature of language and symbol. The symbol '5' or 'V' is not a number, any more than the word 'cat' will ever say "meeow![]() "
"
Children in the elementary grades use "manipulatives" -- match sticks, blocks, etc. -- which are actual numbers, not their representatives. But that quickly outlives its usefulness, and it becomes conventional to speak of the numerals -- 1, 2, 3, and so on -- as the natural numbers; which they are not.
Mathematical existence
As far as mathematics is concerned, in what sense do these natural numbers exist -- and what do we even mean by the question? Do we mean whether five apples or ten trillion stars exist? Obviously, they do. Or do we mean that the idea of any natural number exists; that there is but one number 5, whose yet-to-be-named form, /////, we recognize in things? The mathematician Leopold Kronecker once observed, "God made the natural numbers. Man has made all the rest."
Apart from the idea of a natural number, or the physical existence of one, such as ten fingers, we have the clearest of models for what we call its mathematical existence. It appears in Euclid's Elements, where a figure, such as a circle or a square, will "exist" only when we have drawn it. For it is a principle of logic that we may not assume that what we have defined exists. (We can define a unicorn, but does a unicorn exist?) And so to simply define a "square" according to our idea of one is not enough. Rather, it is our ability to draw a square -- to produce it -- which shows that it is more than just an idea. As with everything in life that begins as an idea, we must bring it into this world. If we cannot, then it is nothing but an idea, which is to say, a fantasy.
Moreover, statements with the word "all" or "every" -- such as "All right angles are equal" -- refer to all which exist, that is, all which we have actually drawn.
Let us apply this to numbers. We say that a number will exist, mathematically, when we name it. Naming will be a form of producing it. If we have not named it, whether in writing, speech, or thought, it does not yet exist.
("Do you mean to say that the number 100 does not exist mathematically until I name it?" That is correct, and you have just named it!)
Hence, expressions such as "all" natural numbers, or "every" natural number, will refer to every one that we name; which in practice is all we ever require.
Number as magnitude
Physical magnitudes -- lengths, say -- are not numbers, yet we assimilate them to the laws of numbers. We measure them. We cannot use the natural numbers, hence we need a kind of number that is itself a magnitude. They will be the positive real numbers. They will be the numbers of measurement.
Now what is a measurement? Let PQ represent some physical
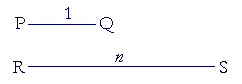
magnitude, say a length; and if it is the unit of measure, say 1 cm, and if RS is a magnitude of the same kind, then the real number n will be the measure of RS when, proportionally,
PQ : RS = 1 : n.
That is what a measurement is: a name for a ratio to the unit of measure, which we name as 1.
Just as a natural number is a collection of units, which we are able to name, so a positive real number is a magnitude whose ratio to 1 we are able to name. The real number is not the ratio itself, which is a relationship with respect to relative size (such as between the base of a triangle and its height). But the real number n names that ratio.
The question, of course, is: Will there always be a name?
The rational numbers
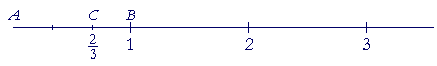
If AB represents the unit magnitude 1, then if AC is two thirds of
| AB, we say that AC is the real number | 2 3 |
("two-thirds"). |
| 2 3 |
is a real number of the first kind, namely a rational number. A |
"rational" number is a magnitude which has the same ratio to 1 that a natural number has to a natural number: the ratio of the numerator to the denominator.
| 2 3 |
: 1 = 2 : 3. |
In English, we name the proper fractions according to that ratio. We call the number we write as 2 over 3 "two-thirds" because of the ratio of 2 to 3: 2 is two thirds of 3. We name the improper fractions analogously.
In these pages, we have respected the distinction between the name for a ratio and the name for a fraction by writing the name of a fraction hyphenated, but the name of a ratio unhyphenated. Thus the number we call two-thirds is two thirds of 1.
| Again, to what does the numeral ' | 2 3 |
' refer? It refers to that magnitude |
| which is two thirds of the unit magnitude 1. There is no ' | 2 3 |
' apart from |
that ratio, apart from the number line above.
(And for whoever might think there is, that symbol has nothing to do with measuring.)
A specific ratio, then, lies behind the numeral for each rational number. To define a rational number only by how it is written (the quotient of two integers), is like defining a cat as that creature whose English name is spelled "c-a-t"![]()
Irrational numbers and their order
A measurement implies a ratio of magnitudes. But magnitudes can be incommensurable. That gives rise to real numbers of the second kind, the irrational numbers. An irrational number does not have the same ratio to 1 that a natural number has to a natural number. An irrational number has no common measure with 1.
Each irrational number -- π, ![]() , ln 2 -- nevertheless names a ratio and hence a measurement. π names the ratio of the circumference of a circle to the diameter.
, ln 2 -- nevertheless names a ratio and hence a measurement. π names the ratio of the circumference of a circle to the diameter. ![]() names the ratio of the diagonal of a square to the side. Every irrational number names at least a ratio to 1.
names the ratio of the diagonal of a square to the side. Every irrational number names at least a ratio to 1.
An irrational number will exist not only on being named, but it must satisfy a property of any "number," namely we must know how to place it with respect to order. Our knowledge of 8, for example, is that it is more than 7 and less than 9. As for an irrational number, we must be able to place it with respect to order relative to any rational number. Is it less than or greater than 2.71828103594612074? That will be our knowledge of an irrational number. In fact, that will be its rational approximation -- which in any case is our only knowledge of an irrational number![]()
For example,
1.414213562373095 < ![]() < 1.414213562373096.
< 1.414213562373096.
You nor anyone else has ever beheld the actual value of ![]() , or e, or any irrational number.
, or e, or any irrational number.
Nameless numbers?
Arithmetic demands a name for a number. We have a system for naming the natural numbers, and therefore we can name any rational number. Apart from unique irrational numbers such as π and e, names for the irrationals come from the categories of functions: roots, sines, arcsines, logarithms, and so on. But names are discrete. On that point alone, it should be clear that there can be no arithmetical continuum -- a continuum of names is an absurdity. Just as it is not possible to name every point on a line, so it not possible that corresponding to every point there is a number. Any claim that there is such a number will have an inherent flaw, namely that there are "numbers" with no names.
In other words, no matter how a real number is defined -- whether as an infinite decimal (whatever that means), or as the limit of a rational sequence (whatever that means) -- the claim that the real numbers constitute a continuum will require the oxymoron, "nameless numbers." They will be "numbers" of which we have no knowledge -- which we could never order relative to any fraction -- and therefore do not exist.
It is not possible, in other words, to name -- to measure -- every length. That is the tension between geometry and arithmetic. That is the separation of geometry and arithmetic.
In fact, if AB is the unit length, and C is an arbitrary point on the

line, then, although AC will have a ratio to AB, the probability that there will be a number to name that ratio, that is, to name the length of AC, is virtually 0.
There is no arithmetical continuum.
Why the insistence on a continuum of numbers? It was a logical attempt for the functions of calculus to be functions of continuous variables, and for the values of those variables to be "numbers," rather than the physical magnitudes length and time themselves. The absence of such a continuum however is not a practical issue. We measure things with rational numbers, anyway. Irrational numbers are an algebraic gateway to them. As for the calculations of calculus, we come up with a number -- which is all we have ever done -- even though the theoretical explanation for what we are doing might be nonsense. (At one time, mathematicians explained calculus in terms of "infinitesimals." And neither Newton nor Leibniz could give an intelligible definition of the derivative![]() )
)
As for the enunciations of the theorems, they can stay as they are, with the understanding that by "all" real numbers, we mean all that we might name or write while doing a problem; that is, all that will actually exist.
The theory of real numbers, then, together with its associated set theory ("The set of real numbers," "The set of points on a line," etc.), are the most prominent current examples of fantasy mathematics.
![]()
www.proyectosalonhogar.com
