1
CONTINUOUS VERSUS
DISCRETE
Calculus began by studying continuous motion in which the speed is not constant. To understand what that means, let us distinguish what is continuous from what is discrete.
A natural number is a collection of discrete units.
![]()
5 pencils, 8 electrons, 100 people. Each one is indivisible. You cannot take half of any one. If you do, it will not be that unit -- that same kind of thing -- any more. Half a person is not also a person!
But consider the distance between A and B. That distance is not
![]()
made up of discrete units. It is not a number of anything. We say, instead, that it is continuous. That means that as we go from A to B, there is no break.
(Continuous does not mean stretches on and on -- "continues"; it means not composed of discrete units. Thus if you study continuously for an hour, you do not take a break.)
Since the length AB is continuous, not only could we take half of it, we could take any part we please -- a tenth, a hundredth, or a billionth -- because AB is not composed of units. And most important, any part of AB, however small, will still be a length.
With a natural number, on the other hand, we can take only certain parts. Of 10 people, we can take only half, a fifth, or a tenth.
The idea of continuous is that there is no limit to smallness.
DEFINITION 1.1. We say that a quantity is continuous if it will have any part, no matter how small, and if each part is itself a quantity of the same kind.
(By a part we mean an aliquot ("a-li-qu't") part, which means that the part is contained in the whole an exact number of times. See Lesson 14 of Arithmetic.)
Whatever is continuous we call a magnitude. And each part will be a magnitude of the same kind. The idea of time, for example, as represented in calculus, is that even a trillionth of a second is still an interval of time.
Length, area, time, speed. We consider these magnitudes. Magnitudes have size, which is to say, we try to measure them.
Our definition of continuous is the classical one from geometry. Compare Euclid's Proposition X.1:
If we are given two unequal magnitudes, a smaller and a larger, and if from the larger we subtract more than half, and from what remains we again subtract more than half, and so on, then eventually we will obtain a magnitude that is less than the smaller.
That will be possible because magnitudes are continuous. We cannot do that with two unequal natural numbers, because we will never obtain a number less than 1.
As an example of continuous motion, think of a car accelerating
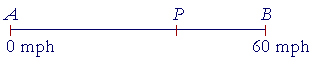
from 0 to 60 mph. At the point A, it has speed of 0 mph, and at the point B it has a speed of 60 mph. Obviously, we would say, in moving from A to B, the speed had every conceivable value between 0 and 60 mph. At some point P, then, it must have had a speed of 37.65026887 mph![]()
The smallness -- of which there is no limit -- is at the eighth decimal place here: .00000007 mph.
That constantly changing speed is an example of a continuum, where values change by infinitesimal degrees. That is a model of what calculus studies.
Problem. Which of these is continuous and which is discrete?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
a) The leaves on a tree. Discrete
b) The stars in the sky. Discrete
c) The distance from here to the Moon. Continuous.
d) A bag of apples. Discrete
e) Applesauce. Continuous!
f) A dozen eggs. Discrete. (But if they're scrambled?)
g) 60 minutes. Continuous. Time is continuous.
h) Pearls on a necklace Discrete
i) The area of a circle.
As area, it is continuous; any part of an area is also an area. But as a form, a circle is discrete; half a circle is not also a circle.
j) The volume of a sphere.
As volume, it is continuous. As a form, a sphere is discrete.
k) A gallon of water.
Continuous. We think of volume as having any part.
But
l) Molecules of water.
Discrete. In other words, if we could keep dividing a quantity of water, then ultimately (in theory) we would come to one molecule. If we divided that, it would no longer be water!
m) A chapter in a book.
Discrete. Surely, half a chapter is not also a chapter.
n) Events.
If you think that half an event is also an event, then you will say that events -- such as a birthday party -- are continuous. (We are not speaking of the time in which the event occurs. We are speaking of the event itself.) Otherwise, you will say that events are discrete.
o) The changing shape of a balloon as it's being inflated.
Continuous. The shape is changing continuously.
p) The evolution of biological forms; that is, from fish to man
n) (according to the theory).
What do you think? Was it like a balloon being inflated? Or was each new form discrete?
q) Words. Discrete.
r) Ideas.
If you think that half an idea is also an idea, (Really?), then you will say that ideas are continuous.
s) The names of numbers.
Surely, the names of anything are discrete. What sense does half a name make?
t) The numbers obtained from actual measurements.
Discrete, because an actual measurement will always produce a terminating decimal. And terminating decimals -- rational numbers -- are discrete. A measurement will never produce square root of 2. That number can be produced only by logic.
u) The universe.
Discrete. Is half a universe also a universe?
Apart from our conceptions of time, space and motion, we see that virtually everything we encounter is discrete. Even a movie -- where the figures on the screen appear to be in continuous motion -- is made up of individual frames, which are discrete.
Calculus, however, is the study of magnitudes; of things that are continuous.
![]()
www.proyectosalonhogar.com
