9
LINEAR FUNCTIONS
The Equation of a Straight Line
Solving a first degree equation
WE NOW BEGIN THE STUDY OF THE GRAPHS of polynomial functions. We will find that the graph of each degree leaves its characteristic signature on the x- y-plane.
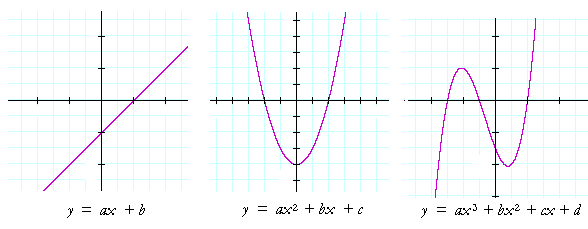
The graph of a first degree polynomial is always a straight line. The graph of a second degree polynomial is a curve known as a parabola. A polynomial of the third degree has the form shown on the right. Skill in analytic geometry consists in recognizing this relationship between equations and their graphs -- hence the student will know that the graph of any first degree polynomial is a straight line, and, conversely, any straight line has for its equation, y =ax + b.
Let us begin with the polynomial function of the first degree:
y = ax + b.
To be specific, let us consider
y = 2x + 4.
A solution to that equation is the ordered pair (1, 6). Because when x = 1 and y = 6, the equation is true:
6 = 2· 1 + 4
Another solution is (0, 4). Because when x = 0 and y = 4, then
4 = 2· 0 + 4,
which again is true.
To find solutions, simply let x have any value you please -- the equation then determines the value of y.
Problem 1. Find three solutions to the first degree equation y = x − 5.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
For example, (0, −5), (1, −4), (−1, −6).
Problem 2. Which of the following ordered pairs solve the equation
y = 2x + 1 ?
(0, −1) (0, 1) (1, 2) (1, 3)
(0, 1) and (1, 3)
Now, since there are two variables x and y, is it possible, on the x-y plane, to draw a "picture" of all the solutions to that equation?
First, let us list a few solutions:
y = 2x + 1
(−1, −1), (0, 1), (1, 3), (2, 5)
And now let us plot these as points on the plane:
We see that all these solutions lie on a straight line. In fact, the x, y coördinates of every point on that line will solve the equation!
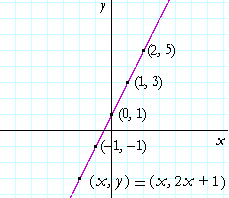
Every coördinate pair (x, y) is
(x, 2x + 1).
y = 2x + 1.
That line, therefore, is called the graph of the equation y = 2x + 1. And y = 2x + 1 is called the equation of that line.
Every first degree equation has for its graph a straight line. (We will prove that below.) For that reason, functions, or equations, of the first degree -- where 1 is the highest exponent -- are called linear functions or equations.
The x- and y-intercepts
The x-intercept of the graph is the solution to the polynomial equation, ax + b = 0.
The y-intercept is the value of y when x = 0. The y-intercept is the constant term, b.
Example 1. Mark the x- and y-intercepts, and sketch the graph of
y = 2x + 6.
Solution.
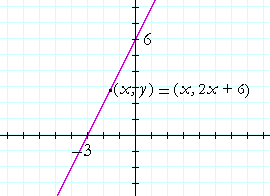
The x-intercept is the root. It is the solution to 2x + 6 = 0. The x-intercept is −3.
The y-intercept is the constant term, 6.
Again, what does it mean to say that y = 2x + 6 is the "equation" of that line?
It means that at every point (x, y) on that line, the y-coördinate is 2 times the x-coördinate, plus 6. Every coördinate pair on that line is (x, 2x + 6).
Problem 3. Mark the x- and y-intercepts, and sketch the graph of
y = −3x − 3
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
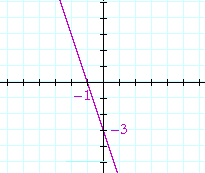
The x-intercept is the solution to −3x − 3 = 0. It is x = −1. The y-intercept is the constant term, −3.
The slope-intercept form
This linear form
y = ax + b
is called the slope-intercept form of the equation of a straight line. Because, as we shall prove presently, a is the slope of the line, and b -- the constant term -- is the y-intercept.
This first degree form
Ax + By + C = 0
where A, B, C are integers, is called the general form of the equation of a straight line.
Theorem. The equation
y = ax + b
is the equation of a straight line with slope a and y-intercept b.
For, a straight line may be specified by giving its slope and the coördinates of one point on it. (Theorem 8.3.)
Therefore, let the slope of a line be a, and let the one point on it be its y-intercept, (0, b).
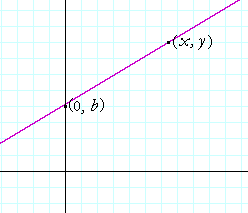
Then if (x, y) are the coördinates of any point on that line, its slope is
| y − b x − 0 |
= | y − b x |
= a. |
On solving for y,
y = ax + b.
Therefore, since the variables x and y are the coördinates of any point on that line, that equation is the equation of a straight line with slope a and y-intercept b. This is what we wanted to prove.
Problem 4. Name the slope of each line, and state the meaning of each slope.
a) y = 2x + 1
The slope is 2. This means that for every unit that x increases, y increases 2 units. Over 1, and up 2.
| b) y = − | 2 3 |
x + 4 |
| The slope is − | 2 3 |
. This means that for every 3 units x increases, |
| y decreases 2 units. Over 3 and down 2. | ||
c) y = x
The slope is 1. This means that for every 1 unit that x increases, y increases 1 unit. This is the identity function, Lesson 5.
d) 3x + 3y = 1
It is only when y = ax + b, that the slope is a. Therefore, on solving for y: y = −x + 1/3. The slope is −1. This means that for every unit the line goes over, it goes down 1.
Next Topic: Quadratics: Polynomials of the 2nd degree
www.proyectosalonhogar.com
