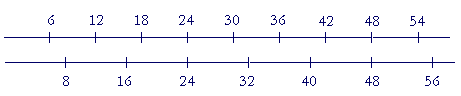|
Lesson 22 COMPARING FRACTIONSIn this Lesson, we will answer the following:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
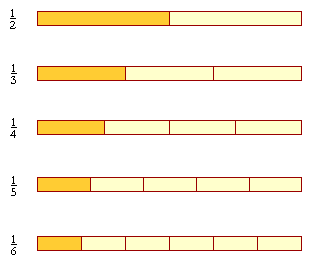
In each of these, the numerator is the same: 1. As the denominators
For, in terms of ratios, if the whole is in 6 pieces, then 1 of 6 pieces --
Further, since one-sixth is smaller than one-fifth, then
Three will be smaller than three:
And so on. When the numerators are the same, then the larger the denominator, the smaller the fraction. In terms of ratios, then the ratio of 1 to 2, for example, is greater than the ratio of 1 to 3: 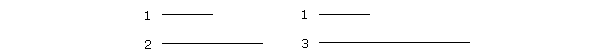
When we compare 1 with 2, it appears greater than when we compare it with 3. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
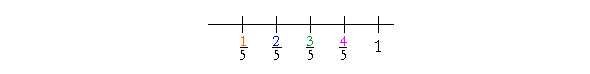
And so on, when the denominators are the same.
As for ratios, we say that the ratio of 2 to 5 is smaller than the ratio of 3 to 5: 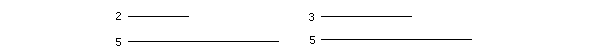
2, when compared with 5, appears smaller than 3 when compared with 5. Example 1. Arrange these from smallest to largest:
numerator; therefore
The sequence is
Lowest common multiple We will now consider fractions in which the numerators and denominators are different. But first, we must learn about the lowest common multiple. Here are the multiples of 6: 6, 12, 18, 24, . . . And here are the multiples of 8: 8, 16, 24, 32, . . . 24 is a common multiple of 6 and 8. It is their lowest common multiple, which we abbreviate as the LCM.
The LCM is the first time that the multiples of 6 meet the multiples of 8. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Example 3. Find the LCM of 9 and 12. Solution. Go through the multiples of 12 until you come to a multiple of 9. 12, 24, 36. 36 is the first multiple of 12 that is also a multiple of 9. 36 is their LCM. Example 4. Find the LCM of 2 and 8.
8 itself is their LCM. When the larger number is itself a multiple of the smaller number, then the larger number itself is their LCM. Example 5. Find the LCM of 5 and 20. Solution. 20 is their LCM. Now the product of two numbers will always be a common multiple. The product of 6 and 4, for example, is 24, and 24 is a common multiple -- but it is not their lowest common multiple. Their lowest common multiple is 12. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Example 6. What is the LCM of 6 and 7? Answer. 1 is their only common divisor. Therefore their LCM is 6 × 7 = 42. (1 is a common divisor of every pair of numbers, but some pairs have 1 as their only common divisor. 6 and 7 are such a pair.) Example 7. What is the LCM of 8 and 12? Answer. 24. Their LCM is not 8 × 12, because 8 and 12 have common divisors besides 1; for example, 4. (To find the LCM from prime factors, see Lesson 32.) We will now see how to compare any two fractions. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Answer. Make a common denominator. Choose the LCM of 2 and 8 -- which is 8 itself. (Example 4, above.)
We see:
That is,
Answer. Again, we will make the denominators the same, and then compare the numerators. As a common denominator, we will choose the LCM of 4 and 32, which is 32 itself.
terms by 8,
Answer. As a common denominator, choose the LCM of 6 and 9. Answer. Choose 18.
both terms by 2. We choose a common multiple of the denominators, because we change denominators by multiplying them.
Adding fractions (as we will see in Lesson 24) involves the same technique as comparing them, because the denominators -- the units -- must be the same. For example,
At this point, please "turn" the page and do some Problems. or Continue on to the next Section. Introduction | Home | Table of Contents Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||