|
COMPARE FRACTIONS Lesson 22 Section 2 The ratio of two fractions In the previous Section, we saw that when two fractions have the same denominator, then the larger the numerator, the larger the fraction.
In other words, Fractions with the same denominator are in the same ratio
We now ask: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Why? Because 16 and 15 are the numerators we would get if we
as
The numerators, 16 and 15, have been obtained by "cross-
we multiplied both terms by 3.)
Answer. On cross-multiplying,
as 2 is to 4. That is,
Answer. On cross-multiplying,
as 36 is to 35. What is more, since 36 is larger than 35, this tells us that
Note: We must begin multiplying with the numerator on the left: 4 × 9. Example 4. What ratio has 1½ to 2?
whole number 2 as a numerator, and cross-multiply:
1½ is three fourths of 2.
For an application of this, see Lesson 26: Multiplying fractions. Example 5. What ratio has 2½ to 3?
as
as 5 is to 6. 2½ is five sixths of 3. More than or less than ½ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
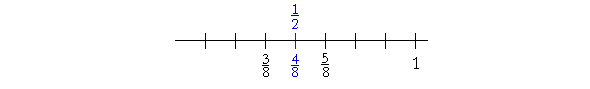
than half of 8.
of 20.
less than half of 25 (which is 12½). (Lesson 15, Question 7.) We could make these comparisons for any ratio of the terms. For example, we could know that
Because 5 is a third of 15, but 6 is less than a third of 21 (which is 7). Example 8. Which is the largest number?
Answer. First, let us examine the list to see if there are numbers less than ½ or greater than ½. We may eliminate any numbers less than (or equal to) ½.
Since the numerators are the same (Section 1, Question 1), we
Example 9. Which is the largest number?
are greater. Which is larger, then,
On cross-multiplying, we have 5 × 11 versus 9 × 6. And 55 is greater than 54. Therfore,
Please "turn" the page and do some Problems. or Continue on to the next Lesson. Introduction | Home | Table of Contents Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
