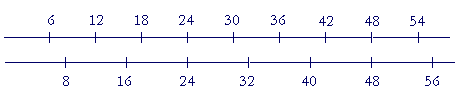S k i l l
i n
A R I T H M E T I C

Lesson 22

COMPARING FRACTIONS

In this Lesson, we will answer the following:

How can we compare fractions with the same numerator?
How can we compare fractions with the same denominator?
How can we find the lowest common multiple of two numbers?
When is the LCM of two numbers simply their product?
How can we compare fractions when the numerators and denominators are different?
Section 2
How can we know the ratio of any two fractions?
How can we know whether a fraction is more than or less than ½?

1.	How can we compare fractions with the same numerator?

	The larger the denominator, the smaller the fraction.

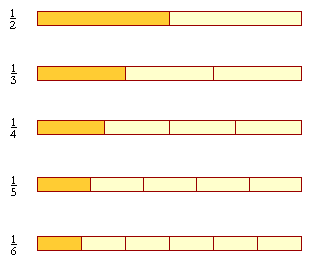
In each of these, the numerator is the same: 1. As the denominators

get larger, then the fraction -- the size of each piece -- gets smaller.

1
6

smaller than

1
5

For, in terms of ratios, if the whole is in 6 pieces, then 1 of 6 pieces --

1
6

-- is smaller than 1 of 5 pieces:

1
5

Further, since one-sixth is smaller than one-fifth, then

2
6

is smaller than

2
5

Three will be smaller than three:

3
6

is smaller than

3
5

And so on.

When the numerators are the same, then the larger the denominator, the smaller the fraction.

In terms of ratios, then the ratio of 1 to 2, for example, is greater than the ratio of 1 to 3: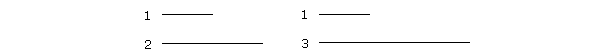

When we compare 1 with 2, it appears greater than when we compare it with 3.

2.	How can we compare fractions with the same denominator?

	The larger the numerator, the larger the fraction.

2
5

is larger than

1
5

. For we're counting units --

1
5

's.

3
5

is larger than

2
5

4
5

is larger than

3
5

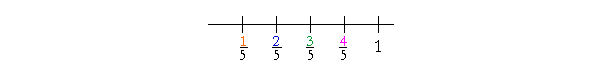
And so on, when the denominators are the same.

Equivalently, 3 out of 5 --

3
5

-- is more than 2 out of 5:

2
5

As for ratios, we say that the ratio of 2 to 5 is smaller than the ratio of 3 to 5: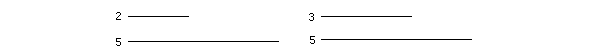

2, when compared with 5, appears smaller than 3 when compared with 5.

Example 1. Arrange these from smallest to largest:

5
7

4
9

4
7

Solution. We must compare them in pairs.

4
9

and

4
7

have the same

numerator; therefore

4
9

is smaller than

4
7

5
7

and

4
7

have the same denominator; therefore

5
7

is larger than

4
7

The sequence is

4
9

4
7

5
7

Example 2. Which is smaller,

1
10

2
9

Answer. Since

1
10

is smaller than

1
9

, then it is surely smaller than

2
9

Lowest common multiple

We will now consider fractions in which the numerators and denominators are different. But first, we must learn about the lowest common multiple.

Here are the multiples of 6:

6, 12, 18, 24, . . .

And here are the multiples of 8:

8, 16, 24, 32, . . .

24 is a common multiple of 6 and 8. It is their lowest common multiple, which we abbreviate as the LCM.

The LCM is the first time that the multiples of 6 meet the multiples of 8.

3.	How can we find the lowest common multiple of two numbers?

	Go through the multiples of the larger number until you come to a multiple of the smaller number.

Example 3. Find the LCM of 9 and 12.

Solution. Go through the multiples of 12 until you come to a multiple of 9.

12, 24, 36.

36 is the first multiple of 12 that is also a multiple of 9. 36 is their LCM.

Example 4. Find the LCM of 2 and 8.

8 itself is their LCM.

When the larger number is itself a multiple of the smaller number, then the larger number itself is their LCM.

Example 5. Find the LCM of 5 and 20.

Solution. 20 is their LCM.

Now the product of two numbers will always be a common multiple. The product of 6 and 4, for example, is 24, and 24 is a common multiple -- but it is not their lowest common multiple. Their lowest common multiple is 12.

4.	When is the LCM of two numbers simply their product?

	When 1 is their only common divisor.

Example 6. What is the LCM of 6 and 7?

Answer. 1 is their only common divisor. Therefore their LCM is 6 × 7 = 42.

(1 is a common divisor of every pair of numbers, but some pairs have 1 as their only common divisor. 6 and 7 are such a pair.)

Example 7. What is the LCM of 8 and 12?

Answer. 24. Their LCM is not 8 × 12, because 8 and 12 have common divisors besides 1; for example, 4.

(To find the LCM from prime factors, see Lesson 32.)

We will now see how to compare any two fractions.

5.	How can we compare fractions when the numerators and denominators are different?

	Change them to equivalent fractions with the same denominator. (Lesson 21.) As the common denominator, choose their LCM. Then, compare the numerators.

Example 8. Which is larger,

1
2

3
8

Answer. Make a common denominator. Choose the LCM of 2 and 8 -- which is 8 itself. (Example 4, above.)

We will change

1
2

to an equivalent fraction with denominator 8:

1
2

4
8

The denominators are now the same, and we can compare

4
8

with

3
8

We see:

4
8

is larger than

3
8

That is,

1
2

is larger than

3
8

Example 9. Which is larger,

3
4

25
32

Answer. Again, we will make the denominators the same, and then compare the numerators. As a common denominator, we will choose the LCM of 4 and 32, which is 32 itself.

We will express

3
4

with denominator 32.

On multiplying both

terms by 8,

3
4

24
32

We are now comparing

3
4

, or

24
32

with

25
32

25 is larger than 24; therefore

25
32

is larger than

3
4

Example 10. Which is larger,

5
6

7
9

Answer. As a common denominator, choose the LCM of 6 and 9.

Answer. Choose 18.

5
6

15
18

7
9

14
18

To change

5
6

, we multiplied both terms by 3. To change

7
9

, we multiplied

both terms by 2.

We choose a common multiple of the denominators, because we change denominators by multiplying them.

Now, 15 is larger than 14. Therefore,

5
6

is larger than

7
9

Adding fractions (as we will see in Lesson 24) involves the same technique as comparing them, because the denominators -- the units -- must be the same. For example,

5 6	+	7 9	=	15 18	+	14 18

			=	29 18	.

At this point, please "turn" the page and do some Problems.

Continue on to the next Section.

Introduction | Home | Table of Contents