S k i l l
i n
A R I T H M E T I C

Lesson 21

EQUIVALENT FRACTIONS

In this Lesson, we will answer the following:

What are equivalent fractions?
How can we know when fractions are equivalent?
How do we reduce a fraction to its lowest terms?
Section 2
How can we reduce a fraction in which the numerator or denominator is a decimal?

1.	What are equivalent fractions?

	Fractions that have the same value, or are at the same place on the number line.

Example 1.

1
2

and

2
4

are equivalent. They are at the same cut

in the number line.

2.	How can we know when fractions are equivalent?

	Their numerators and denominators are in the same ratio.

The student who has not learned about ratios (Lesson 16) may nevertheless benefit from the summary below.

Example 2.

1
2

2
4

because each numerator has the same ratio to its

denominator, namely half.

Any fraction where the numerator is half of the denominator will be

equivalent to

1
2

2
4

3
6

5
10

8
16

1 is half of 2. 2 is half of 4. 3 is half of 6. And so on. These are all at the same place on the number line. Each number is half of 1.

In terms of equal ratios, if a pie is cut into 2 pieces and you eat 1 of them, you will get just as stuffed as when the pie is in 4 pieces and you eat 2; or if you eat 4 out of 8, or 5 out of 10, and so on. In each case, you have eaten an equivalent "fraction" of the pie, namely half.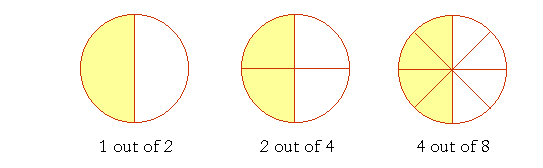

Example 3. Write the missing numerator:

7
21

?
12

Answer. 7 is a third of 21. A third of 12 is 4.

7
21

4
12

7 is to 21 as 4 is to 12.

7
21

and

4
12

are equivalent fractions.

Example 4. Write the missing numerator:

3
7

?
35

Answer. Here, we will look alternately (Lesson 17, Question 2). To make 35, 7 has been multiplied by 5. Therefore, 3 also must be multiplied by 5:

3
7

5 × 3
35

5 × 7

This is the theorem of the same multiple.

Everything that we know about ratios carries over into fractions, because each numerator has a ratio to its denominator.

Example 5.

9
50

is equal to what decimal?

Answer. A decimal is a fraction whose denominator is understood to be a power of 10: 10, 100, 1000, etc. We can easily make the denominator 50 into 100 by multiplying it by 2. Therefore we must also multiply 9 by 2:

9
50

18
100

= .18

Hundredths is two decimal places. (Lesson 2, Question 5.)

3.	How do we reduce a fraction to its lowest terms?

	Divide both terms by a common divisor.

Example 6. Reduce to lowest terms:

20
24

Answer. 20 and 24 have a common divisor, 4.

20
24

"4 goes into 20 five times."
6

"4 goes into 24 six times."

This is the Theorem of the Common Divisor. (Lesson 16, Question 7.)

Example 7. Reduce

500
1500

Answer. When the terms have the same number of 0's, we may ignore them.

500
1500

5
15

1
3

Effectively, we have divided 500 and 1500 by 100. (Lesson 1, Question 11.)

Example 8. Write as a mixed number:

20
8

Solution. Divide 20 by 8. "8 goes into 20 two (2) times (16) with 4 left over."

4
8

is equal to

1
2

Alternatively, we could reduce first. 20 and 8 have a common divisor 4:

20 8	=	5 "4 goes into 20 five times." 2 "4 goes into 8 two times."

	=	2½.

Notice that we are free to interpret the same symbol

20
8

in various ways. It is the fraction

20
8

. It is the ratio of 20 to 8. And it is

20 divided by 8.

Example 9. Reduce

5
5

Answer.

5
5

= 1.

Any fraction in which the numerator and denominator are equal, is equal to 1.


Summary

1)	We look directly at the ratio of the numerator to the denominator.

	Each numerator is a third of the denominator.
2)	We multiply both terms by the same number.

	Both 2 and 3 have been multiplied by 5.
3)	We divide both terms by the same number.

	Both 10 and 15 have been divided by 5.

At this point, please "turn" the page and do some Problems.

Continue on to the next Section.

Introduction | Home | Table of Contents