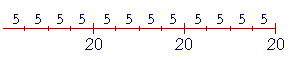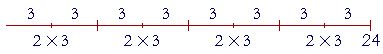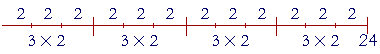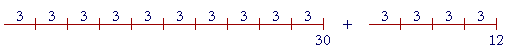THE MEANING OF DIVISIONLesson 10 Section 2 Some properties of division
(45 × 100) ÷ 100 = 45. And (4500 ÷ 100) × 100 = 4500. The parentheses indicate to do the operation they enclose first. We will explain below why that is true .
Also,
For an explanation why that is true, see below. Example 1. The divisor a decimal. How many times is .2 contained in 6?
The divisor must be a whole number. Therefore, to make .2 into a whole number, multiply it by 10. Multiply 6 by 10 also:
Why did we multiply by 100? Because that makes the divisor .03 a whole number. In other words: If the divisor is a decimal, multiply it by 10, or 100,
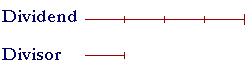
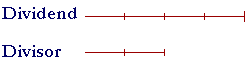
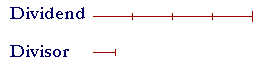
on dividing 12 by 2. Or,
on dividing 8 by 2. Or, finally,
These three possibilities imply: The order in which we multiply or divide does not matter. For the explanation why that is true, see below. We can use this property if we can find a multiple of the divisor within the dividend.
For an explanation why that is true, see below. The following, and final, property leads to a simple method for dividing mentally. Decomposing the dividend
In other words, If we can express the dividend as a sum or difference of multiples This is called decomposing the dividend. It follows from the following theorem: If a number is a divisor of two numbers, then it will also be a divisor For the explanation why that is true, see below. Example 3. Decomposing the dividend.
What number divisible by 5 is close to 8? 5 itself. And since 5 is divisible by 5, so is 50. What must we add to 50 to get 85? 35. Therefore decompose 85 into 50 + 35.
85 is made up of Seventeen 5's. Ten 5's (50) + Seven 5's (35). The point is to decompose -- break up -- 85 into any multiples of 5 that you know. For example, 75 + 10 -- if you know how many 5's there are in 75. This is division by decomposing the dividend. And you can understand it. See below. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Example 6. Divide $96 equally among 4 people. Answer. We have to divide 96 by 4. To do that, we will break 96 up into two numbers that are obviously divisible by 4. Now, which multiple of 4 less than 9 is closest to 9? 8. And since 8 is divisible by 4, then so is 80. To make 96 we need to add 16. Therefore, we will decompose 96 into 80 + 16:
96 is made up of Twenty-four 4's. Alternatively, we could have expressed 96 as 100 − 4. If we divide each of those by 4, we get 25 − 1 = 24. Example 7. 265 is made up of how many 5's? Answer. We want to break up 265 into obvious multiples of 5. Now, which multiple of 5 is closest to the first two digits of 265? The multiple of 5 closest to 26 is 25. And since 25 is divisible by 5, so is 250. Therefore, decompose 265 as 250 + 15. Then,
265 is made up of Fifty-three 5's. Fifty 5's + Three 5's. With a little practice, this will be a mental calculation. Example 8. 6 CD's that cost the same, together cost $114. How much did each one cost?
Each one cost $19. In this case, it was convenient to express 114 as the difference, 120 − 6. Example 9. A business spent $2,580 on items that cost $6 each. How many items did they buy? Answer. What number times 6 is 2,580? We must divide 2580 by 6. Since 24 is divisible by 6, then so is 2400.
We can check this -- and any division -- by multiplying. 430 × 6 = 400 × 6 + 30 × 6 = 2400 + 180 = 2580 (Lesson 8) Example 10. You have $840 from which you have to make monthly payments of $75. How many $75 payments can you make? Solution. There are at least ten 75's in 840: 10 × 75 = 750. And 750 plus another 75 is 825. 15 more will make 840.
You could make 11 payments of $75. And $15 would remain. Example 11. Inexact division.
"5 goes into 22 four (4) times with 2 left over." Write the remainder 2 as the numerator of the fraction.
In the next Lesson, we will see that it is on this principle of decomposing the dividend that the historical written method is based. Explanation of the properties of division Arithmetic is the first science. We look at facts themselves. We will explain the properties of division by looking at the arithmetical meanings of multiplication and division, and the relationship between them. This is not algebra.
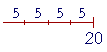
To illustrate that, let us start with 5, and then multiply it by 3:
3 × 5 And now, let us divide by 3. Let us repeatedly subtract 3's. But since 15 is now composed of 5's, how can we do that? According to the order property of multiplication, 3 × 5 = 5 × 3.
And so the product is made up of 3's -- it is made up of five 3's. 15 ÷ 3 = 5. Hence we are back where we started, at 5. The student should realize that the multiplication table -- 3 × 5 = 15 -- is not the point here. The point is to understand -- to see -- that while 3 × 5 is a sum of 5's, we can still subtract 3's. This property, after all, holds for any numbers. (206 × 19) ÷ 19 = 206. Understanding that has nothing to do with knowing the "answer" to 206 × 19 Next, let us start with 15 and divide it by 5:
We will get 3, because 3 × 5 = 15. But according to the order property, 5 × 3 = 15.
Therefore, if we now multiply 3 by 5, we will get back to 15
The quotient is the number of times the divisor is contained in the dividend. As many times, then, as we increase or decrease the dividend -- and keep the divisor the same -- the quotient will increase or decrease that same number of times. If we double the dividend, the divisor will go in twice as many times, that is, the quotient will double. If we triple the dividend, the quotient will triple. On the other hand, if we divide the dividend by 2, that is, is we take half of it -- -- then quotient will also be half. And so on. Next, as many times as we increase or decrease the divisor -- and keep the dividend the same -- the quotient will decrease or increase that same number of times. If we double the divisor, the quotient will be half. If we triple the divisor, the quotient will be one third as much. On the other hand, if we divide the divisor by 2 -- -- it will go in twice as many times. If we divide the divisor by 3, the quotient will triple. And so on. Therefore, if we increase or decrease the dividend and the divisor the same number of times, the quotient will not change. In other words: The quotient will not change if we multiply the dividend and divisor by the same number, or if we divide them both by the same number.
(3 × 20) ÷ 5 = 3 × (20 ÷ 5) That is, to divide 3 × 20 by 5, we may first divide 5 into 20, and then multiply by 3. Here is (3 × 20) ÷ 5 -- Three 20's divided by 5:
But that is the same as (20 ÷ 5) --
-- added three times! Therefore, (3 × 20) ÷ 5 = 3 × (20 ÷ 5)
For example, to divide 24 by (2 ×3), we may first divide by 2, and then divide that quotient by 3 24 ÷ (2 × 3) = (24 ÷ 2) ÷ 3. Here is 24 ÷ (2 × 3):
Here is 24 ÷ 2:
We now want to divide this by 3. We want to count the 3's in this figure. Now each group of Three 2's is a threesome -- it is a 3. And there are as many of those 3's in the bottom figure as there are (2 × 3)'s in the top figure. Count them! 24 ÷ (2 × 3) [The top figure] = (24 ÷ 2) ÷ 3 [The bottom figure].
For example, (30 + 12) ÷ 3 = (30 ÷ 3) + (12 ÷ 3)
30 contains 3 ten times. 12 contains 3 four times. Therefore, 30 + 12 contains 3 ten + four = fourteen times. Please "turn" the page and do some Problems. or Return to Section 1. or Continue on to the next Lesson. Introduction | Home | Table of Contents Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||