Now we ignored a total of three 0's. Therefore we must put back those three 0's:
For a number does not change if we divide it and then multiply the quotient by the same number.
Example 8. Multiplying by 11. 11 × 45.
Multiplication by 11 is particularly easy, because 11 = 10 + 1. Therefore, 11 × 45 is equal to 10 × 45 + 1 × 45:
450 + 45 = 495.
Example 9. 11 × 6.2 = 62 + 6.2 = 68.2
To do this or any of these problems in writing --
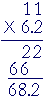
-- is nothing more than a trick to get the right answer.
Example 10. How much
is 13 × 12?
Answer. If you know that
12 × 12 = 144,
then 13 × 12 is simply one more
12:
13 × 12 = 144 + 12 = 156
(Lesson 4,
Question 3.)
Or, we could count the 12's like this:
|
Thirteen 12's
|
= Ten 12's + Three 12's
|
| |
|
|
= 120 + 36
|
|
| |
|
|
= 156.
|
This is the property of adding multiples of a number, which we can express it as follows:
A sum of units does not depend on the unit.
In other words, 2 units + 3 units = 5 units, no matter what the unit. 2 chairs + 3 chairs = 5 chairs. And 2 nines + 3 nines = 5 nines.
(Since this is true in arithmetic, the right-hand distributive law of algebra may be applied to arithmetic.)
How to square a number mentally
A square figure is a four-sided figure in which all the sides are equal, and

all the angles are right angles.
To square a number means to multiply it by itself.
"9 squared" = 9 × 9 = 81.
To find the area of a square figure -- that is, the space enclosed by the four straight lines -- square the length of a side. (See Lesson 9.) If each side were measured by number 6, for example, then the area would be measured by 6 × 6 = 36.
Now, say that we want to square a two-digit number such as 24, mentally. The following geometrical arithmetic illustrates how.
Look at this square figure in which each side is 24.
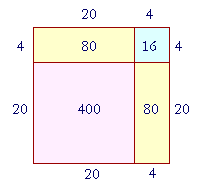
Then the area of that square will be 24 × 24. But we can break up 24 into 20 + 4. Therefore the entire square will be composed of the following:
The square of 20, which is 400.
Two rectangles, each with area 20 × 4 = 80.
And the square of 4, which is 16.
In other words, the square of 20 + 4 is equal to
The square of 20, plus
Two times 20 × 4, plus
The square of 4.
400 + 160 + 16 = 576.
This is not a difficult mental calculation.
Example 11. Square 52.
Solution. 52 = 50 + 2.
The square of 50 + 2 is equal to
The square of 50, plus
Two times 50 × 2, plus
The square of 2.
2500 + 200 + 4 = 2704.
Problem 1. Square 35.
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
The square of 30 + 5 is equal to:
The square of 30 + Two times 30 × 5 + The square of 5.
900 + 300 + 25 = 1225.
Example 12. Square 48.
Solution. Rather than square 40 + 8, it is simpler to square 50 − 2. In this case, the square of 50 − 2 equals
The square of 50, minus
Two times 50 × 2, plus
The square of 2.
2500 − 200 + 4 = 2304.
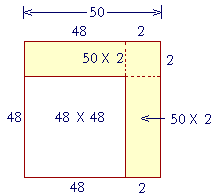
The entire square is the square of 50. It is composed of the square of 48, plus two rectangles, 50 × 2 -- which we must subtract. But we should not subtract the square of 2 twice. Therefore we add it at the end.
Problem 2. Square 39.
The square of 40 − 1 is equal to:
The square of 40 − Two times 40 × 1 + The square of 1.
1600 − 80 + 1 = 1521.
At this point, please "turn" the page and do some Problems.
or
Continue on to the Section 2:
The distributive property
Introduction | Home | Table of Contents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com