|
The numbers exactly divisible by 3 are the multiples of 3:
3, 6, 9, 12, and so on.
And since these are divisible by 3, so are
30, 60, 90, 120, . . .
300, 600, 900, 1200, . . .
The numbers exactly divisible by 8 are the multiples of 8:
8, 16, 24, 32, . . .
80, 160, 240, 320, . . .
800, 1600, 2400, 3200, . . .
The figure below illustrates that 8 goes into 32 exactly. 32 is a multiple of 8.
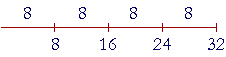
But 8 does not go into 35 exactly:
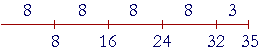
35 is not a multiple of 8. There is a remainder of 3.
35 ÷ 8 = 4 R 3
The remainder is what we have to add to the multiple of 8 to get 35.
35 = 4 × 8 + 3
Possible remainders
Say that there is a large group of people, and we want to divide them into groups of 5.

But say we discover that there is not an exact multiple of 5. Then how many people might we not be able to group? How many people might remain?
Answer: Either 1, or 2, or 3, or 4. Because if more than 4 remained, we could make another group of 5!
The point is:
The remainder is always less than the divisor.
If we divide by 5, then the possible remainders are 1, 2, 3, or 4.
Example 8.
a) If 7 is the divisor, what are the possible remainders?
Answer. 1, 2, 3, 4, 5, 6.
b) How many 7's are there in 61?
Answer. 8. And there is a remainder of 5.
61 ÷ 7 = 8 R 5
That is,
61 = 8 × 7 + 5
Example 9. Prove: 47 ÷ 9 = 5 R 2
Proof. 47 = 5 × 9 + 2.
Example 10. Divide 53 by 8. Write the whole number quotient and the remainder.
Answer. 53 ÷ 8 = 6 R 5
8 goes into 53 six (6) times: 48. What must we add to 48 to get 53?
5.
48 + 5 = 53.
5 is the remainder.
See Problems 6 - 10.
The division bar
In what follows, we will signify division in this way:
"16 divided by 8 is 2."
Dividend
Divisor
|
= Quotient |
The test is:
Quotient × Divisor = Dividend
The short horizontal line is called the division bar. The division bar is also used to signify a fraction, because a fraction indicates division of the numerator by the denominator. (Lessons 19 and 23.) We also use the division bar to signify the ratio of two numbers. (Lesson 16.)
"280 divided by 7 is what number?"
Answer. Ignore the 0. 7 goes into 28 four (4) times. Therefore 7 goes into 280 forty (40) times.
40 times 7 is 280.
(Lesson 8, Question 2.)
In other words, since 28 is divisible by 7, then so is '28' followed by any number of 0's.
280 2800 28,000 280,000 . . .
Answer. 600. Because 600 × 9 = 5400.
| Example 13. |
246
100 |
= |
2.46 |
This is 246 ÷ 100. (Lesson 3)
| 5 ÷ 8 is simply the fraction |
5
8 |
-- which we can interpret as 5 ÷ 8 |
because of the division bar
In the next Lesson we will see how to express 5 ÷ 8 as a decimal.
In Lesson 31, Prime numbers, we will learn about the divisors of a number.
Section 2: Some properties of division
Introduction | Home | Table of Contents
www.proyectosalonhogar.com
|