Powers of 10, Section 2 -- A complete course in arithmetic

S k i l l
i n
A R I T H M E T I C

POWERS OF 10

Lesson 1 Section 2

5.	What is a unit?

	Whatever we call one.

A unit is that by virtue of which every thing that exists
is called one.

(Euclid, Book VII, Definition 1.)

If we are counting chairs -- "1 chair, 2 chairs, 3 chairs" -- then a chair is the unit. If we are counting hours -- "1 hour, 2 hours," and so on -- then an hour is the unit. Even if we just write "5," we mean five units --

-- even though we do not say the word "units." For there is no "5" apart from 5 units.

If we count by tens -- 10, 20, 30, 40, 50 -- then 10 is the unit; if we count by hundreds -- 100, 200, 300 -- then 100 is the unit; while if we count by quarters -- 1 quarter, 2 quarters, 3 quarters (of an hour, say) -- then that fractional part is the unit.

A unit, we could say, is whatever has a name. We count only things that have the same name, which is to say, we must recognize whether something is the same or different. ("Here's one; here's one. This is not one.")

Example 1. Let 5 be the unit and count to 30.

Answer. "5, 10, 15, 20, 25, 30."

Example 2. Let

1
8

be the unit, and count to

7
8

Answer. ^"

1
8

2
8

3
8

4
8

5
8

6
8

7
8

.^"

Example 3.	42	=	40 + 2

-- no matter what the unit.

42 eggs		=	40 eggs + 2 eggs

42 tens		=	40 tens + 2 tens

42 hundreds		=	40 hundreds + 2 hundreds

And so on. For again there is no "42" apart from 42 units, even though we do not say the word "units."

Place value

Say that we have a very, very large number of blocks.

And say that we organize them as follows. First, we group them into as many hundreds as we can.

We then group the rest into as many tens as we can. (There will be less than 10 tens, because that would have been another hundred.) And so we will be left with a number that is less than ten.

Say that we find:

3 Hundreds + 6 Tens + 4 Ones

In other words, we found 364 blocks:

364 = 3 Hundreds + 6 Tens + 4 Ones

This illustrates that in our system of writing numbers, apart from the Ones on the right, the units are the powers of 10. That is, there are 3 of that unit (Hundreds), plus 6 of that one (Tens), plus 4 of those (Ones). Each place belongs to a different unit.

Every whole number, then, implies a sum.

364 = 3 Hundreds + 6 Tens + 4 Ones,

That is called the expanded form of 364.

6.	What does it mean to write a number in expanded form?

	It means to show the unit -- the power of 10 -- at each digit's place.

Example. Write 7,328 in expanded form.

Answer. Write

7,328 = 7 Thousands + 3 Hundreds + 2 Tens + 8 Ones

In practice, however, it is often more useful to expand the number in this way:

7,328 = 7,000 + 300 + 20 + 8

See Lesson 8.

7.	What do we mean by the place value of a digit?
2,658
	Starting with ones on the right, it is the power of 10 at each digit's place.

Example 1. In this number

439,072,658

what is the place value of 0?

Answer. Hundred thousand.

For, in each class of three digits, there are Ones, Tens, and Hundreds.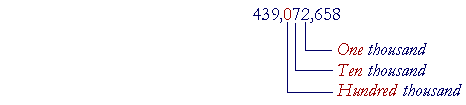

0 is in the class of thousands and in the Hundreds place. Its place value
-- the power of 10 at that position -- is Hundred thousand.

Example 2. In this number

386,214,035

how many Ten millions are there?

Answer. 8. For, on counting from the right, the millions are the third group of three digits, 386. The Tens place is the middle one (Ones, Tens, Hundreds). There are 8 Ten millions.

To prepare for the standard written methods of addition and subtraction, we ask the following:

8.	What is the relationship between units of adjacent place value?
Thousands Hundreds Tens Ones
	10 units of lower value can be composed -- gathered together -- to make 1 unit of the next higher value.

10 ones = 1 ten.

10 Ones can be composed into 1 Ten.

10 Tens can be composed into 1 Hundred.

10 Hundreds can be composed into 1 Thousand.

And so on.

Equivalently,

1 unit of higher value can be decomposed -- broken up - into 10 units of the next lower value.

Thousand Hundreds Tens Ones

1 Thousand can be decomposed into 10 Hundreds.

1 Hundred can be decomposed into 10 Tens.

1 Ten can be decomposed into 10 Ones.

Thousands Hundreds Tens Ones

We will see this when we come to regrouping in addition and subtraction.

Rounding off

9.	How do we round off, or approximate, a whole number to a given place?
1,2651,300
	Look at the digit to the right of the given place. If it is a 5 or greater, add 1 to the given place. If it is less than 5, leave the given place unchanged. In either case, replace all the digits to the right of the given place with 0's.

Example 1. Round off 6,528 to the nearest ten.

Answer. 6,5286,530

(The wavy equal signmeans "is approximately equal to.")

2 is in the tens place. To round off to the nearest ten, look at the digit to the right: 8 (greater than 5). Therefore, add 1 to the tens place. Replace 8 with 0.

Example 2. Round off 6,528 to the nearest hundred.

Answer. 6,5286,500

5 is in the hundreds place. To round off to the nearest hundred, look at the digit to the right: 2 (less than 5). Therefore, leave the hundreds place unchaged. Replace 28 with 00.

Example 3. Round off 6,528 to the nearest thousand.

Answer. 6,5287,000

6 is in the thousands place. To round off to the nearest thousand, look at the digit to the right: 5. Therefore, add 1 to the thousands place. Replace 528 with 000.

Example 4. Round off 79,521 to the nearest thousand.

Answer. 79,52180,000

9 is in the thousands place. To round off to the nearest thousand, look at the digit to the right: 5. Therefore, add 1 to 79 -- it becomes 80. Replace 521 with 000.

To round off decimals, see Lesson 11.

At this point, please "turn" the page and do some Problems.

Continue on to the next Section.

Section 1 of this Lesson

Introduction | Home | Table of Contents

Please make a donation to keep TheMathPage online.
Even $1 will help.

Questions or comments?

E-mail: themathpage@nyc.rr.com