|
Lesson 1 POWERS OF 10Our system of writing numbers is based on the powers of 10, and so it is here that we begin. Before starting the Lessons, though, the student should begin mastering both Elementary Addition and the Multiplication Table. In this Lesson, we will answer the following:
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Examples. 405 is a three-digit number. The digits are 4, 0, and 5. 38 ends in the digit 8. $612 has the same digits as $6.12. Those ten marks are also known as the Arabic numerals, because it was the Arab mathematicians who introduced them into Europe, where their forms evolved. |
|||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||
|
10 × 1 = 10 10 × 10 = 100 10 × 100 = 1000 And so on. The Powers of 10
Strictly, 1 is not a power of 10. The first power of 10 is 10 itself. It has one 0. The second power of 10 is 100; it has two 0's. And so on. Notice how the names fall into groups of three: One thousand, Ten thousand, Hundred thousand. One million, Ten million, Hundred million. Each group of three -- Ones, Tens, Hundreds -- is called a class. |
|||||||||||||||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||||||||||||||
|
Each class is named after the first number in that class. Starting with billions (bi for two), each class has a Latin prefix. For easy reading, each class -- each group of three digits -- is separated by commas. With the assumption that the student can read any number from 1 to 999, we can now answer the following: |
|||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Example 1. Read this number: 256,312,785,649,408,163 Answer. Starting from the left, 256, read each three-digit group. Then say the name of the class. 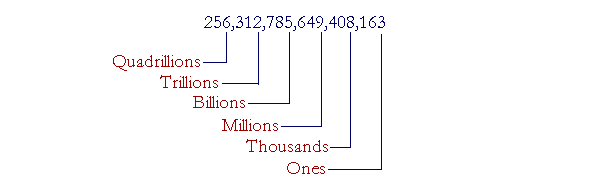
Say: "256 Quadrillion, 312 Trillion, 785 Billion, 649 Million, 408 Thousand, 163." Do not say the class name "Ones." The class of Ones, on the right, are the numbers 1 through 999. Together with the class names, they are the only numbers we need to know how to read. Example 2. Place commas in this number to distinguish the classes: 8792456 Answer. Starting from the right, place commas every three digits: 8,792,456 Read the number: "8 million, 792 thousand, 456." Example 3. Read this number: 7,000,020,002 Answer. "Seven billion , twenty thousand, two." When a class is absent, we do not say its name; we do not say, "Seven billion, no million, ..." Also, every class has three digits and so we must distinguish the following:
As for "and," in speech it is common to say "Six hundred and nine," but in writing we should reserve "and" for the decimal point, as we will see in the next Lesson. (For example, we should write $609.50 as "Six hundred nine dollars and fifty cents." Not "Six hundred and nine dollars.") Example 4. Write in numerals: Four hundred eight million, twenty-nine thousand, three hundred fifty-six. Answer. Pick out the classes: "million", "thousand". Each class (except perhaps the first class on the left) has exactly three digits: 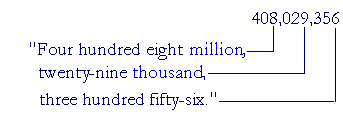
Example 5. Write in numerals: Five billion, sixteen thousand, nine. Answer. After the billions, we expect the millions, but it is absent. Therefore write 5,000,016,009 Again, we must write "sixteen thousand" as 016; and "nine" as 009; because each class must have three digits. The exception is the class on the extreme left. We may write "Five" as 5 rather than 005. When writing a four-digit number, such as four thousand five hundred, it is permissible to omit the comma and write 4500. In fact, we often read that as "Forty-five hundred." But when a number has more than four digits, then for the sake of clarity we should always place the commas. Example 6. Distinguish the following:
At this point, please "turn" the page and do some Problems. or Continue on to Section 2. Introduction | Home | Table of Contents www.proyectosalonhogar.com |
|||||||||||||||||||||||||||||||||||||||||||||
