|
RATIO AND PROPORTION 1 Lesson 16 Section 3 |
||||||||
| ||||||||
|
Example 1. What ratio has 2 to 3? Answer. "2 is two thirds of 3." 2 says its cardinal name, "Two." 3 says its ordinal name, "third." That is how to express the ratio of any smaller number to a larger. Example 2. What ratio has 4 to 5? Answer. "4 is four fifths of 5." To see this, consider that 1 is one fifth of 5: 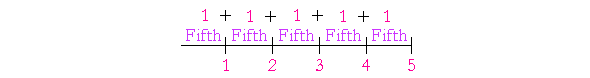
2 is two fifths of 5. 3 is three fifths of 5. 4 is four fifths of 5. Each number says its name. Lowest terms The two numbers of a ratio are called its terms. In the ratio of 4 to 12, |
||||||||
|
||||||||
|
Many pairs of numbers have the same ratio as 4 and 12, for example. 4 is to 12 as 1 is to 3. Now, it is perfectly correct to say, "4 is four twelfths of 12." But when we say, "4 is one third of 12," then we have expressed that ratio with the lowest terms, that is, with the smallest numbers which have that ratio. The terms 1 and 3 say their names. |
||||||||
|
||||||||
|
Example 3. The ratio of 7 to 8 expressed as seven eighths is with the lowest terms, because 1 is the only common divisor of 7 and 8. But the ratio of 12 to 18 expressed as twelve eighteenths, although true, is not with the lowest terms, because 12 and 18 have a common divisor 6. |
||||||||
|
||||||||
|
(In the next Lesson, we will see why.) Example 4. What ratio has 12 to 18? Answer. 12 and 18 have a common divisor 6: "6 goes into 12 two times and into 18 three times." The quotients are 2 and 3. Therefore according to the theorem, 12 is to 18 as 2 is to 3. "12 is two thirds of 18." 
2 and 3 say their names. Example 5. Express the ratio of 21 to 28 with the lowest terms. Answer. Their ratio will be expressed with a sentence, "21 is 28." 21 and 28 have a common divisor 7: "7 goes into 21 three times and into 28 four times." 21 is to 28 as 3 is to 4. "21 is three fourths of 28." 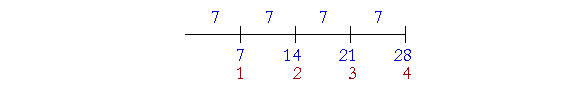
Notice that their common divisor, 7, is one fourth of 28. Example 6. If a is an eighth of b, then a is to b as ? is to ?. Complete that proportion with the smallest numbers -- the lowest terms -- which have that ratio. Answer. There are many pairs such that the first is an eighth of the second. 2 and 16; 5 and 40; 10 and 80. However, the smallest such numbers are 1 and 8. If a is an eighth of b, then a is to b as 1 is to 8. Example 7. Numbers that end in the same number of 0's. What ratio has 800 to 2400? Answer. If two numbers end in the same number of 0's, then we may ignore those 0's and take the ratio of what remains. Both 800 and 2400 end in two 0's. Therefore 800 is to 2400 as 8 is to 24. 8 is a third of 24. Therefore, 800 is a third of 2400. Why may we ignore the 0's? Because when we do, we have divided both terms by the same power of 10. The quotients will have the same ratio as the numbers divided. Example 8. What ratio has 400 to 50? Answer. Since 400 is larger than 50, it will be so many times 50. Now, 50 ends in only one 0, therefore we may ignore only one 0: 400 is to 50 as 40 is to 5. 40 is eight times 5. Therefore 400 is eight times 50. Please "turn" the page and do some Problems. or Introduction | Home | Table of Contents Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
||||||||
