(Euclid, VII. 17.)
Example 5. Complete this proportion:
Solution. Look at it alternately. To produce 12, the term 6 has been multiplied by 2. Therefore, 7 must also be multiplied by 2:
6
7 |
= |
12
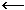 2 × 6
2 × 6
14 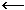 2 × 7
2 × 7
|
Example 6
. Complete this proportion:
Solution. 3 has been multiplied by 6. Therefore, 2 also must be multiplied by 6:
2
3 |
= |
12
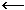 6 × 2
6 × 2
18 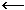 6 × 3
6 × 3
|
In fact, consider these columns of the multiples of 2 and 3:
2 3
4 6
6 9
8 12
10 15
12 18
14 21
And so on.
Now 2 is two thirds of 3. (Lesson 16.) And as 2 is to 3, so each multiple of 2 is to that same multiple of 3:
4 is two thirds of 6.
6 is two thirds of 9.
8 is two thirds of 12.
And so on. In fact, these are the only natural numbers where the first will be two thirds of the second.
Example 7. Name three pairs of numbers such that the first is three fifths of the second.
Solution. The elementary such pair are 3 and 5. To generate others, take the same multiple of both: 6 and 10, 9 and 15, 12 and 20, and so on.
Example 8. 27 is three fourths of what number?
Solution. Only a multiple of 3 can be three fourths of another number, which must be the same multiple of 4.
As 3 is to 4, so 27 is to ?
Since 27 is 9 × 3, therefore the missing term is 9 × 4:
As 3 is to 4, so 27 is to 36.
27 is three fourths of 36.
Example 9. Complete this proportion:
Solution. Here, we must look directly:
9 is a fifth of 45. And 2 is a fifth of 10.
Example 10. Complete this proportion:
Solution. Looking alternately, we see that 200 has been divided by 2. Therefore 12 also must be divided by 2:
12
200 |
= |
6
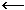 12 ÷ 2
12 ÷ 2
100 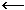 200 ÷ 2
200 ÷ 2
|
|
Summary
|
|
To solve a proportion alternately, either both terms must be divided by the same number, as in the example above, or, as in Examples 5 - 8, both terms must be multiplied by the same number.
|
|

As for the Theorem of the Common Divisor, it is a restatement of the Theorem of the Same Multiple. For, this proportion,
6 is to 100 as 12 is to 200,
where the 3rd and 4th terms appear as doubles of the 1st and 2nd, is logically equivalent to this proportion,
12 is to 200 as 6 is to 100,
where the 3rd and 4th terms appear as halves of the 1st and 2nd.
Example 11. In a class, the ratio of girls to boys is 3 to 4. (This means there are 3 girls in the class for every 4 boys.) There are 24 boys. How many girls are there?
Solution 1. "The ratio of girls to boys is 3 to 4." What ratio has 3 to 4? 3 is three fourths of 4. (Lesson 16.) Therefore, the number of girls is three fourths of the number of boys -- three fourths of 24. One fourth of 24 is 6. Therefore, three fourths are 18.
(See Lesson 14, Questions 4 and 5.)
Solution 2. Proportionally,
Note that 24 corresponds to the boys.
Now, 24 is 6 × 4. Therefore, the number of girls is 6 × 3 = 18.
Example 12. The whole is equal to the sum of the parts. In a class, the ratio of girls to boys is 3 to 4. There are 35 students. How many girls are there and how many boys?
Answer. To say that the ratio of girls to boys is 3 to 4, is to say that 3 out of every 7 students are girls (3 + 4 = 7), and 4 out of every 7 are boys. In other words, three sevenths of the students are girls, and four sevenths are boys.
Now, one seventh of 35 is 5. Therefore three sevenths are 3 × 5 = 15. There are 15 girls. The rest, then, -- 20 -- are boys.
We could also answer by forming a proportion:
There are 15 girls. Hence there are 20 boys.