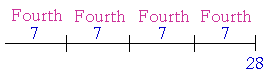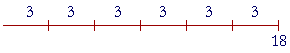|
Lesson 14 PARTS
|
||||||||||||||
|
||||||||||||||
|
The natural numbers have two forms, cardinal and ordinal. The cardinal forms are One, two, three, four, etc. They answer the question How much? or How many?. The ordinal forms are First, second, third, fourth, etc. They answer the question Which one?. A natural number is a collection of indivisible ones.
5 pencils, 8 electrons, 100 people. You cannot take half of any one. By a "number" in what follows, we will mean a natural number. |
||||||||||||||
|
||||||||||||||
|
The natural numbers, then, are the multiples of 1: 1, 2, 3, 4, 5, 6, and so on, for as far as we please. Here are the multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, . . . 5 is the first multiple of 5; 10 is the second; 15, the third; and so on. |
||||||||||||||
|
||||||||||||||
|
5, then, is a certain part of each its multiples, except itself. 5 is a certain part of 10, a part of 15, of 20, etc. (We do not call 5 a part of 12, because 12 is not a multiple of 5. We are speaking throughout of what is called an aliquot part.) Here again are the multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, . . . Now, since 15 is the third multiple of 5, we say that 5 is the third part of 15. We use that same ordinal number to name the part.
5 is contained in 15 three times. Therefore we say "5 is the third part of 15." That is which part of fifteen 5 is. Similarly, 5 is the fourth part of 20. It is the fifth part of 25, the sixth part of 30; and so on. But, 5 is half of 10. (We do not say the second part.) And 5 is not a part of itself; there is no such thing as the first part. It is important to understand that we are not speaking here of proper fractions -- numbers that are less than 1, and that we need for measuring. We are explaining how the ordinal numbers --- third, fourth, fifth, etc. -- name the parts of the cardinal numbers. When answering the questions of this Lesson, the student should not write fractions. We will come to those symbols in Lesson 19. The parts in any case are prior to the fractions, because
That must be understood first. We can then explain that
In Lesson 10 we learned about dividing a number into equal parts. We can now say into which parts the number has been divided: into thirds, fourths, fifths, sixths -- or halves. Example 1. 3 is which part of 18?
Answer. 3 is the sixth part of 18. We say that because 18 is made up of six 3's. Example 2. What number is the fourth part, or a quarter, of 28? Answer. 7. Because 28 is made up of four sevens.
Example 3. 2 is the fifth part of what number? Answer. 10. Because five 2's are 10.
Every number is the fifth part of 5 times itself. 4 is the fifth part of 5 × 4 = 20. 9 is the fifth part of 5 × 9 = 45. 20 is the fifth part of 5 × 20 = 100. Example 4. Find all the divisors of 30 in pairs. That is, find all the numbers that go into 30 exactly. Each divisor (except 30) is which part of 30? Answer. Here are all the divisors of 30 in pairs: 1 and 30. (Because 1 × 30 = 30.) 2 and 15. (Because 2 × 15 = 30.) 3 and 10. (Because 3 × 10 = 30.) 5 and 6. (Because 5 × 6 = 30.) On naming which part of 30, each divisor will say the ordinal name of its partner:
1 is the thirtieth part of 30. 2 is the fifteenth part of 30. 15 is half of 30. 3 is the tenth part of 30. 10 is the third part of 30. 5 is the sixth part of 30. 6 is the fifth part of 30. Note that 1 is a part of every natural number (except 1 itself), because every natural number is a multiple of 1. That is what a natural number is. 1 is that part which says the number's name.
1 is the third part of 3, the fourth part of 4, the fifth part of 5, the hundredth part of 100. 1 is half of 2. Thus divisors always come in pairs. 3 and 6, for example, are a pair of divisors of 18, because 3 × 6 = 18. What is more, 3 is the sixth part of 18, while 6 is the third part. This implies the following: Theorem. For every divisor (except 1) that a number has, it will have a part with the ordinal name of that divisor. (Euclid, VII. 37.) Since 18 has a divisor 3, then 18 has a third part. And since 18 has a divisor 6, then 18 has a sixth part. Here is an illustration that 18 has a divisor 3:
18 = 6 × 3. But according to the order property of multiplication: 18 = 3 × 6.
This means that 6 -- the partner of 3 -- is the third part of 18. Therefore since 18 has a divisor 3, then 18 has a third part. * When we say "5 is the third part of 15," we do not imply a sequence of parts: the first part, the second part, the third part, and so on. This is a different meaning for the word "third." It means each one of three equal parts that together make up the whole.
We say that we have divided 15 into thirds. Yet "third" still retains an ordinal character. Because to the question, "Which part of 15 is 5?", we answer, At this point, please "turn" the page and do some Problems. or Continue on to the next Section: Parts, plural Introduction | Home | Table of Contents Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
||||||||||||||