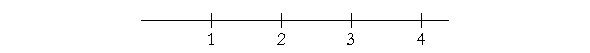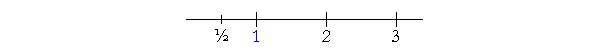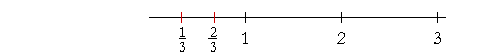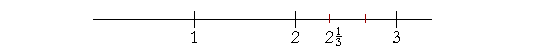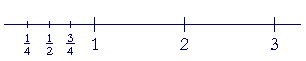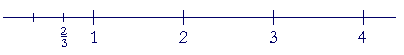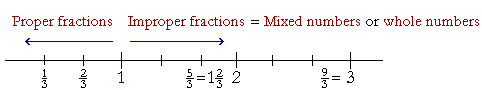|
Lesson 19
COMMON FRACTIONS
PROPER FRACTIONS
MIXED NUMBERS
IMPROPER FRACTIONS
By a natural number we have meant a collection of indivisible ones.

A natural number has only certain parts. 6, for example, has only half, a third part, and a sixth part. The natural number 1 has no parts -- we cannot take half of 1 person!
But if we now think of 1 as being like a length,

then it will have any part -- half, third, fourth, fifth, millionth!
This gives rise to a new and different kind of number -- a fraction. It is a number we need for measuring rather than counting. We are then able to say that a certain length, for example, is 5¼ cm. And so what we call a proper fraction is a number less than 1.
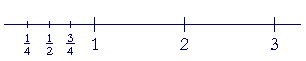
Fractions belong to what is continuous rather than what is discrete. See The Evolution of the Real Numbers, Lesson 3.
We will see that everything we have learned about ratios will apply to fractions, because, as we will see, each numerator has a ratio to its denominator. And the fraction itself is a number that has a ratio to 1.
In this Lesson, we will answer the following:
- What is a common fraction?
- What is a proper fraction?
- How can we recognize a proper fraction?
- How are the proper fractions named?
- What ratio has each fraction to 1?
- What is a mixed number?
- What is an improper fraction?
- How can we express an improper fraction as a mixed number?
- How can we express a mixed number as an improper fraction?
|
|
1.
|
What is a common fraction?
|
| |
|
|
A number written with a numerator and a denominator, in which both are natural numbers.
|
|
|
Example 1.
|
3
10 |
is a common fraction. It is in contrast to .3, which is |
a decimal fraction, or simply a decimal.
| The numerator
of |
3
10 |
is 3. The denominator is 10. These are the
|
terms of the fraction. We will see that they correspond to the terms of a ratio.
|
|
2.
|
What is a proper fraction?
|
|
|
|
|
A fraction that is less than 1.
|
|
|
|
3.
|
How can we recognize a proper fraction?
|
|
|
|
|
The numerator is smaller than the denominator.
|
|
2
3 |
("two-thirds") is a proper fraction. It is less than 1. |
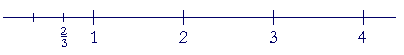
| On the number line, it falls to the left of 1. Specifically, |
2
3 |
is two thirds |
of 1, as we will see presently.
|
|
4.
|
How are the proper fractions named?
|
|
|
|
|
The same as the ratio of the numerator to the denominator.
|
|
|
Example 2.
The number we write as 1 over 2 --
|
1
2 |
-- is called
|
"one-half" because of the ratio of 1 to 2. 1 is one half of 2.
We write the name of the number hyphentated --
one-half -- but the name of the ratio unhyphenated. Obviously, one must first understand what it means to say that a number is one half of 1. That is, one must first understand ratio.
|
Example 3. Why is this number
|
3
4 |
called "three-fourths"?
|
Answer. Because of the ratio of 3 to 4. 3 is three fourths of 4.

This naming is true in English. Spanish is much more scrupulous in distinguishing the names of the fractions from the names of the ratios. This fraction 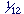 , for example, is called un dozavo, while the ratio of 1 to 12 is la duodécima parte. , for example, is called un dozavo, while the ratio of 1 to 12 is la duodécima parte.
A ratio is a relationship between numbers; numbers have ratios to one another. We will maintain that distinction by writing the name of the number, the fraction, hyphenated, but the ratio unhyphenated. This separation of number and ratio gives life to the question, Can "the ratio of two lengths" (whatever that means) always be named? Is there a number? For, numbers have names. 1, 9.6, 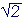 , ,  . If we merely postulate that corresponding to every ratio there always is a number, then we will miss one of the most intriguing and disturbing questions in mathematics. . If we merely postulate that corresponding to every ratio there always is a number, then we will miss one of the most intriguing and disturbing questions in mathematics.
The interested student is referred to The Evolution of The Real Numbers.
Example 4. Read these
numbers:
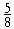
|
"Five-eighths"
|
|
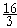
|
"Sixteen-thirds"
|
The improper fractions (see below) are named like the proper fractions.
|
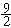
|
"Nine-halves"
|
(Not "Nine 2's.")
|
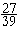
|
"27 over 39"
|
With large numbers, it is not necessary to say "27 thirty-ninths."
|
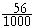
|
"56 thousandths"
|
When the denominator is a power of 10, however, we always say the decimal name. (Lesson 2)
|
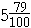
|
"5 and 79 hundredths"
|
This is a mixed number; see below.
|
Ratio to 1
A fraction is a number, and as any number, we know it relative to 1.
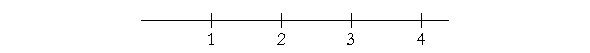
What is our understanding of "2"? It is twice as much as 1. What is "3"? It is three times 1.
Every number has a ratio to 1. It is according to that ratio that we know each number.
What ratio, then, has ½ to 1?
½ is one half of 1.
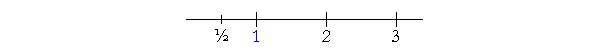
½ has the same ratio to 1 as the numerator has to the denominator.
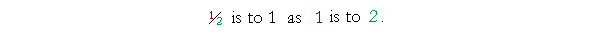
|
|
5.
|
What ratio has each fraction to 1?
|
| |
|
|
The same ratio that the numerator has to the denominator.
|
|
|
Example 5. What ratio has
|
2
3 |
to 1?
|
|
Answer. The number we write as 2 over 3 -- |
2
3 |
-- is two thirds of 1.
|
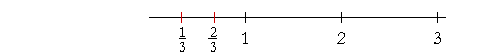
This is the same ratio that 2 has to 3.
| To place |
2
3 |
on the number line, we must cut the length representing 1 |
into three equal pieces. Notice that to cut that unit into thirds, we cut it only twice. "One third, two thirds."
Since the numerator is to the denominator in the same ratio as two natural numbers, fractions are also called rational numbers.
Example 6. This number ¼ is called "one-quarter" or "one-fourth," because the numerator is one quarter of the denominator -- and ¼ itself is one quarter of 1.
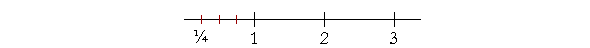
To place ¼ on the number line, we cut the line one less than the name of the part. To divide 1 into fourths, cut the line three times.
Example 7. What number is at the arrow?

Answer. The unit has been cut five times -- into six equal pieces.
The proper fractions are the parts of 1.
The fraction ½ is one half only of 1. But the ratio one half relates many numbers. "5 is one half of 10." "6 is one half of 12." And so on. To write "6 is ½ of 12," as unfortunately some do, is a vulgarism.
|
|
6. |
What is a mixed number?
|
| |
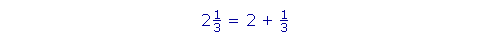
|
| |
A whole number plus a proper fraction.
|
|
| Example 8. 2 |
1
3 |
-- "2 and one-third" -- is a mixed number. It is 2 plus |
1
3 |
. |
The and in "2 and one-third" means plus.
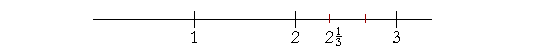
| To place 2 |
1
3 |
on the number line, the unit between 2 and 3 must be cut |
into thirds. We cut the line twice.
Problem. Answer with a mixed number or with a whole number and a remainder, whichever makes sense.
a) How many basketball teams -- 5 on a team -- can you make from 23
a) students?
b) You are going on a trip of 23 miles, and you have gone a fifth of the
b) distance. How far have you gone?
Answers.

|
|
7.
|
What is an improper fraction?
|
| |

|
|
|
A fraction greater than or equal to 1.
|
|
We can recognize an improper fraction when the numerator is greater than or equal to the denominator.
|
Example 9.
Since |
3
3 |
is equal to 1, then |
8
3 |
is greater than 1. |
8
3 |
is an |
improper fraction.
3
3 |
is also called an improper fraction. |
We will now see explicitly why we use the division bar to signify a fraction.
|
|
8.
|
How can we express an improper fraction as a mixed number or a whole number?
|

|
|
|
Divide the numerator by the denominator. Write the quotient (4), and write the remainder (1) as the numerator of the fraction; the denominator stays the same.
|
|
"5 goes into 43 eight (8) times (40) with 3 left over."
The student should not have to write the division box. (Lesson 12.)
"9 goes into 32 three (3) times (27) with remainder 5."
The remainder is what we must add to 27 to get 32. (Lesson 10.)
"4 goes into 28 seven (7) times exactly."
|
|
9.
|
How can we express a mixed number as an improper fraction?
|

|
|
|
Multiply the whole number (4) by the denominator (2), and add the numerator (1).
Write that sum (9) as the numerator of the improper fraction. The denominator stays the same. |
|
|
"5 times 2 is 10, plus 3 is 13; over 5."
"8 times 3 is 24, plus 5 is 29; over 8."
To summarize: Fractions that are less than 1 are called proper fractions, while fractions greater than or equal to 1 are improper. Improper fractions are equivalent to mixed numbers or whole numbers.
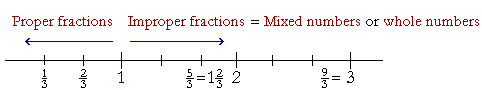
Please "turn" the page and do some Problems.
or
Continue on to the next Lesson.
Introduction | Home | Table of Contents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com
|