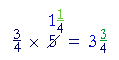|
Lesson 26 THE MEANING OF MULTIPLYING FRACTIONSPARTS OF FRACTIONSIn this Lesson, we will answer the following:
In the previous Lesson we simply stated the rule for multiplying one fraction by another. In this Lesson, we want to understand where that rule comes from. It comes from what multiplying by a fraction means. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For, according to the meaning of multiplication, we are to repeatedly add the multiplicand as many times as there are 1's in the multiplier. In the multiplier ½ there is one half of 1. Therefore we are to add the multiplicand 8 one half a time. We are to take one half of 8. Furthermore, although ½ × 8 looks like multiplication, there is nothing to multiply! To take half of 8, we divide by 2 (Lesson 15). And we begin to see why we have the cancellation rules. For the most general definition of multiplication, see below.

One third of 21 is 7 -- "3 goes into 21 seven (7) times." 2 × 7 = 14.
"One eighth of 32 is 4 . 5 × 4 = 20."
Solution. Although 5 is not exactly divisible by 4, we can still take its fourth part. We can divide by 4:
"4 goes into 5 one (1) time with 1 left over."
Alternatively, we can multiply first:
"4 goes into 15 three (3 ) times (12) with 3 left over. The order in which we multiply or divide does not matter. (Lesson 10) Example 4. You are going on a a trip of four miles, and you have gone two thirds of the way. How far have you gone? Solution. We must take two thirds of 4:
Since 4 is not exactly divisible by 3, we will multiply first:
"3 goes into 8 two (2) times (6) with 2 left over." But again, we could take a third of 4 first: 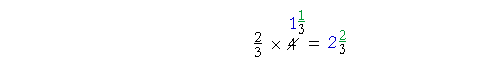
Example 5. How much is a third of 2?
bar. Therefore, we could write immediately:
Example 6. How much is a fifth of 9?
Example 7. How much money is 64 quarters? Answer. 64 quarters would be 64 × $.25. But according to the order property of multiplication, 64 × .25 = .25 × 64
evaluate 64 quarters by taking one quarter of 64! And we can do that by taking half of half. (Lesson 15, Question 8.) Half of 64 is 32. Half of 32 is 16. Therefore 64 quarters are $16. Example 8. A slot machine at a casino paid 93 quarters. How much money is that? Answer. To find a quarter of 93 is equivalent to dividing 93 by 4. (Lesson 15.) We can easily do that mentally by decomposing 93 into multiples of 4. For example: 93 = 80 + 12 + 1. On dividing each term by 4, we have 20 + 3 + ¼ = 23¼. 93 quarters, then, are $23.25. Example 9. A recipe calls for 3 cups of flour and 4 cups of milk. Proportionally, how much milk should you use if a) you use 1½ cups of flour? b) you use 2 cups of flour? c) you use 2½ cups of flour? Answers. a) 1½ cups flour are half of 3 cups. Therefore you should use half as
b) 2 cups flour are two thirds of 3 cups. Therefore you should use two
c) What ratio has 2½ cups of flour to the original 3 cups?
multiplying:
2½ cups are five sixths of 3 cups. Therefore, you should use five sixths of 4 cups of milk.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
We saw this in Lesson 15, Question 1 as a mixed number of times. Example 10. 2½ × 8.
In multiplication, when one of the numbers is a whole number, it is not necessary to change to an improper fraction. (See also the previous Lesson, Question 1.) Example 11. Mental calculation. What is the price of 12 items at $3.25 each? Answer. 12 × $3.25 is the same as $3.25 × 12, or, 3¼ × 12:
Example 12. Multiplying by numbers ending in 5. Calculate mentally: 75 × 6. Answer. Rather than 75 × 6, let us do 7.5 × 6 that is, 7½ × 6. 7½ × 6 = 42 + 3 = 45. Now, by replacing 75 with 7.5, we divided by 10. (Lesson 3, 75 × 6 =450. Example 13. 35 × 16 Answer. 3.5 × 16 = 48 + 8 = 56. Therefore, 35 × 16 = 560. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
That is how to change any number to a percent (Lesson 3).
Solution. 100% is the whole. Therefore, take one eleventh of 100%:
"11 goes into 100 nine (9) times (99) with 1 left over."
See the previous Lesson, Example 3.
Here is the most general definition of multiplication: Whatever ratio the
multiplier has to 1
Consider this multiplication of whole numbers: 3 × 8 = 24 The multiplier 3 is three times 1; therefore the product will be three times the multiplicand; it will be three times 8. Similarly, to make sense out of ½ × 8, the multiplier ½ is half of 1 (Lesson 15, Question 6); therefore the product will be half of 8. Proportionally, As the Multiplier is to 1, so the Product is Or inversely, As 1 is to the Multiplier, so the Multiplicand is The Product, then, is the fourth proportional to 1, the Multiplier, and the Multiplicand. At this point, please "turn" the page and do some Problems. or Continue on to the next Section. Introduction | Home | Table of Contents Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||