|
Lesson 3 Section 2 The Meaning of Percent The student should first understand Section 1: Multiplying and Dividing by Powers of 10.
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
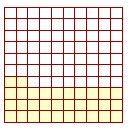
Thus, 100% means 100 for each 100, which is to say, all. 100% of 12 is all of 12. 50% is another way of saying half, because 50% means 50 for each 100, which is half. 50% of 12 is 6. Example 1. Below are 100 squares, and 32 have been shaded.
What percent of the squares have been shaded? Answer. 32% -- 32 for each 100. When the percent is less than or equal to 100%, then we can say "out of" 100. 32% is 32 out of 100. (But to say that 200% is 200 out of 100 makes no sense. 200% is 200 for each 100, which is to say, twice as much.) Example 2. 100 people were surveyed, and 65 responded Yes. What percent responded Yes? Answer. 65% -- 65 out of 100. Example 3. In a class of 30 students, all 30 came to school by bus. What percent came to school by bus? Answer. 100%. 100% means all. (30 for each 30 is equivalent to 100 for each 100.) |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
1% = 1 for each 100. Examples.
Problem 1. How much is 1% of $400? How much is 2% of $400? How much is 3%? How much is 9%? Answer. 1% of $400 is $4.00. Separate two decimal places. Now, 2% is twice as much as 1%. Therefore 2% of $400 is $8. 3% is $12. 4% would be $16. 9%, therefore, is 9 × $4 = $36. Problem 2. How much is 8% of $600? Answer. Since 1% is $6.00, then 8% is 8 × $6.00 = $48.00. Problem 3. How much is 2% of $325? How much is 3%? 4%? Answer. We can get everything from 1%, which is $3.25. 2%, therefore, is $6.50. 3% is $9.75. And 4% is 4 × $3.25 = 4 × $3 + 4 × $.25 = $12 + $1 = $13. These are problems that do not require a calculator. They should be done mentally! |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||

Examples. Problem. How much is 20% of $80? How much is 30%? How much is 90% Answer. 20% is twice as much as 10%. Since 10% of $80 is $8, then 20% is 2 × $8 = $16. 30% is 3 × $8 = $24. 90% is 9 × $8 = $72. The meaning of percent continues in Lesson 14 and Lesson 27. |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
(This is often called changing a percent to a decimal.) 24% = .24 Divide by 100 -- separate two decimal places. For, 24% -- 24 for each 100 -- means 24 hundredths. Division by 100 is indicated by the percent sign itself %, with its division slash / and two 0's. Here are more examples:
Strictly, a percent is not a number, it is a ratio (Lesson 27). Therefore we should speak rather of a number representing a percent. That becomes necessary only for certain written calculations. |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
Examples.
Number to a Percent
.24 = 24%
Percent to a Number Please "turn" the page and do some Problems. or Continue on to the next Lesson. Introduction | Home | Table of Contents Please make a donation to keep TheMathPage online. Copyright © 2001-2007 Lawrence Spector Questions or comments? E-mail: themathpage@nyc.rr.com |
|||||||||||||||||||||||||