Two thirds of 12, then, are equivalent to 8 out of 12.
We can illustrate this with any number that has a fourth part, namely, any multiple of 4. For example, 12, 40, 100:
Percent: Parts of 100%
Percent is another way of expressing a part. Since 100% is the whole (Lesson 3, Question 7), and since 50% is half of 100%, then 50% means half.
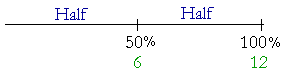
50% of 12 -- half of 12 -- is 6.
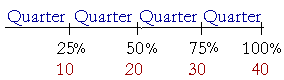
Since 25% is a quarter of 100%, then 25% is another way of saying a quarter. A quarter of 40 -- 25% of 40 -- is 10.
Since 75% is three quarters of 100%, then 75% means three quarters. 30 is 75% of 40.
Whatever part or parts the percent is of 100%, that is the part or parts we mean.
Fifths
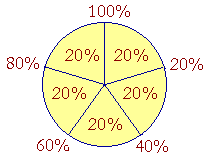
Let the circle represent 100%, and let us divide it into fifths, that is, into 20's. Each 20% is a fifth of the circle. 40%, then, is two fifths of the circle. 60% is three fifths. 80% is four fifths.
That is what those percentages mean:
20% means one fifth.
40% means two fifths.
60% means three fifths.
80% means four fifths.
100% is the whole; it is all five fifths.
How much, then, is 60% of 45?
Answer. 60% means three fifths. To name three fifths, we must first name one fifth. One fifth of 45 is 9. Therefore three fifths are three 9's: 27.
In general, since percent is how many for each 100, then percents are hundredths.
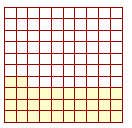
32 of those 100 squares have been shaded. That is, 32%, or 32 hundredths, of them have been shaded.
*
Finally, we will state this theorem:
Each number is either a part of a larger number
or parts of it.
|
(Euclid, VII.4.)
We will illustrate this with each number less than 9. We will see that each number less than 9 is either a part of 9 or parts of 9.
Now, 9 units can be divided either into Ninths or Thirds:
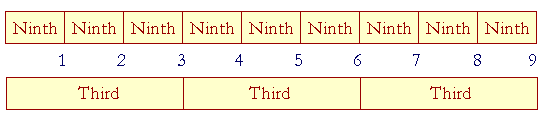
(If 9 is divided into Ninths, then it is divided into 1's. If 9 is divided into Thirds, then it is divided into 3's: 3, 6, 9.)
Let us now see how to relate each number to 9.
1 is the ninth part -- or one ninth -- of 9.
2 is two ninth parts of 9.
(The point again is that each 1 is a ninth part of 9.)
3 is three ninths of 9 -- and also the third part of 9.
4 is four ninths of 9. Count them!
5 is five ninths of 9.
6 is six ninths -- and also two thirds -- of 9. 3 + 3.
7 is seven ninths of 9.
8 is eight ninths of 9.
Notice again how each number says its name:
1 is one ninth of 9.
2 is two ninths of 9.
3 is three ninths of 9.
The first number says its cardinal name. 9 says its ordinal name.
Each number less than 9, then, is either a part of 9 or parts of it. We can therefore express in words how each number is related to 9. We can say that 5, for example, is "five ninths" of 9.
Example 4. What relationship has 9 to 10?
Answer. If we divide 10 into 1's, then each 1 is a tenth part of 10.
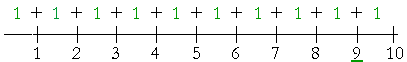
1 is one tenth of 10.
2 is two tenths of 10.
3 is three tenths of 10. And so on, until we come to 9:
9 is nine tenths of 10.
Again, the numbers 9 and 10 say their names. 9 says its cardinal name "nine." 10 says its ordinal name "tenth."
Please "turn" the page and do some
Problems.
or
Continue on to the next Lesson.
Previous Section
Introduction | Home | Table of Contents
Please make a donation to keep TheMathPage online.
Even $1 will help.
Copyright © 2001-2007 Lawrence Spector
Questions or comments?
E-mail: themathpage@nyc.rr.com