1
ALGEBRAIC EXPRESSIONS
The four operations and their signs
ALGEBRA IS A METHOD OF WRITTEN CALCULATIONS that help us reason about numbers. In algebra we use letters as well as numbers, but the letters represent numbers. For example, if we write
a + b = b + a,
then the letter a simply means the first number -- whatever it might be. Letter b means the second number. This is a "rule" that tells us that the order in which we add doesn't matter. This will be true for any numbers, not just for 7 + 3 or for 8½ + 2¼.
In algebra, we imitate with letters what we could write with numbers. The numbers are the numerical symbols, while the letters are called literal symbols.
Question 1. What are the four operations of arithmetic, and
what are their operation signs?
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| 1) | Addition: a + b. The operation sign is + . |
| 1) | For example, if a represents 3, and b represents 4, then a + b represents 7. |
| 2) | Subtraction: a − b. The operation sign is − . |
| 1) | If a represents 8, for example, and b represents 2, then a − b represents 6. |
3) Multiplication: a· b or ab.
2· 5 = 10
"2 times 5 equals 10."
The operation sign is a centered dot. When there is no operation sign, as an ab or 2x, it always means multiplication.
We do not use the multiplication cross × because we do not want to confuse it with the letter x.
Do not confuse the centered dot -- 2·5, which in the United States means multiplication -- with the decimal point: 2.5.
| 4) | Division: | a b |
In algebra, we rarely use the division sign ÷ . We use the division bar.
| 10 2 |
= 5 |
"10 divided by 2 is 5."
Note: In algebra we call a + b a "sum" even though we do not name an answer.
| Similarly, we call a − b a difference, ab a product, and | a b |
a quotient. |
Question 2. What is the function of parentheses () in algebra?
3 + (4 + 5) 3(4 + 5)
Parentheses signify that we should treat what is enclosed
as one number.
3 + (4 + 5) = 3 + 9 = 12. 3(4 + 5) = 3· 9 = 27
Note: Since there is no operation sign between 3 and (4 + 5), it means multiplication.
Problem 1. Distinguish the following:
a) 8 − (3 + 2) b) 8 − 3 + 2
To see the answer, pass your mouse over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
a) 8 − (3 + 2) = 8 − 5 = 3.
b) 8 − 3 + 2 = 5 + 2 = 7.
In a), we treat 3 + 2 as one number. In b), we do not. We first subtract and then add. (But see the order of operations below.)
Question 3. Terms versus factors.
When numbers are added or subtracted, they are called terms.
When numbers are multiplied, they are called factors.
Here is a series of four terms: a − b + c − d.
Here is a product of four factors: abcd.
The word factors always signifies multiplication.
And again, we speak of the "product" abcd, even though we do not name an answer.
Problem 2.
a) In the following expression, how many terms are there?
2a + 4ab + 5a(b + c)
Three. 2a is the first term. 4ab is the second. And 5a(b + c) is all one term.
b) In each term, there are how many factors?
2a has two factors, 2 and a. 4ab has three factors. And
5a(b + c) also has three factors: 5, a, and (b + c).
Powers and exponents
When a number is repeatedly multiplied by itself, we get the powers of that number. Thus, a· a is called the second power of a, or "a squared." a· a· a is the third power of a, or "a cubed." aaaa is a to the fourth power, and so on. The first power of a is a itself.
Now, rather than write aaaa, we write a just once and place a small number 4: a4 ( "a to the 4th"). That small 4 is called an exponent. It indicates the number of times to repeat a as a factor.
Thus, 83 ("8 to the third") means 8· 8· 8.
Problem 3. Read, then calculate each of the following.
a) 5² "5 to the second power" or "5 squared" = 25.
b) 23 "2 to the third power" or "2 cubed" = 8.
c) 104 "10 to the fourth" = 10,000.
d) 121 "12 to the first" = 12.
Question 4. When there are several operations,
8 + 4(2 + 3)² − 7,
what is the order of operations?
Before answering, let us note that since competence in science is the reason for requiring students to learn algebra, and since sequences of operations appear only in certain forms, in these pages we present only those sequences that the student is even remotely likely to encounter in the actual practice of algebra. The division sign ÷ is never used in scientific formulas, and the multiplication cross × is used only in scientific notation -- therefore the student will never see the following:
3 + 6 × (5 + 3) ÷ 3 − 8
Such a problem would be purely academic.
The order of operations is as follows:
(1) Evaluate the parentheses, if there are any.
(2) Evaluate the powers, that is, the exponents.
(3) Multiply or divide -- it does not matter.
(4) Add or subtract.
In the first example below, we will see in what sense we may add or subtract. And in the second example we will encounter multiply or divide.
Example 1. 8 + 4(2 + 3)² − 7
First, we will evaluate the parentheses, that is, we will replace 2 + 3 with 5:
= 8 + 4· 5² − 7
Since there is now just one number, 5, it is not necessary to write parentheses.
Notice that we transform one element, the parentheses, and rewrite all the rest.
Next, evaluate the exponents:
= 8 + 4· 25 − 7
Now multiply:
= 8 + 100 − 7
Finally, add or subtract, it will not matter. If we add first:
= 108 − 7 = 101.
While if we subtract first:
8 + 100 − 7 = 8 + 93 = 101.
| Example 2. | 11· 35 5 |
There are no parentheses to evaluate and no exponents. Next in the sequence is multiply or divide. We may do either -- we will get the same answer. But it is usually more skillful to divide first, because we will then have smaller numbers to multiply. Therefore, we will first divide 35 by 5:
| 11· 35 5 |
= | 11· 7 |
| = | 77 | |
See: Skill in Arithmetic, The properties of division, Property 3.
Example 3. ½(3 + 4)12 = ½· 7· 12.
Now the order of factors does not matter: abc = bac = cab, etc. Therefore we may first do ½· 12. That is, we may first divide 12 by 2:
½· 7· 12 = 7· 6 = 42
| Example 4. The division bar. | 8 + 20 10 − 3 |
In any problem in which there are plus or minus signs in the top and bottom, we must evaluate the top and bottom before we can divide. In other words, we must interpret the top and bottom as being in parentheses.
| 8 + 20 10 − 3 |
means | (8 + 20) (10 − 3) |
. |
Now we proceed as usual and evaluate the parentheses first. The answer is 4.
Problem 4. Evaluate each of the following according to the order of operations.
| a) | 3 + 4· 5 = | b) | 2 + 3· 4 + 5 = | ||
| 3 + 20 = 23 | 2 + 12 + 5 = 19 | ||||
| c) | 4 + 5(2 + 6) = | d) | (4 + 5)(2 + 6) = | ||
| 4 + 5· 8 = 4 + 40 = 44 | 9· 8 = 72 | ||||
| e) | 11· 10 5 |
f) | ½(3 + 4)8 = | ||
| 11· 2 = 22 We may divide first. |
½· 7· 8 = 7· 4 = 28. (½· 8 = 4) Skill in Arithmetic: Lesson 26, Question 1 |
||||
| g) | 2 + 2· 3² 14 − 3· 2² |
= | 2 + 2· 9 14 − 3· 4 |
= | 2 + 18 14 − 12 |
= | 20 2 |
= | 10. |
Question 5. What do we mean by the value of a letter?
The value of a letter is a number. It is the number that will replace the letter when we do the arithmetic.
Question 6. What does it mean to evaluate an expression?
It means to replace each letter with its value, and then do the sequence of operations.
Example. Let x = 10, y = 4, z = 2. Evaluate the following.
| a) x + yz | = | 10 + 4· 2 | b) (x + y)z | = | (10 + 4)2 | |
| = | 10 + 8 | = | 14· 2 | |||
| = | 18. | = | 28. | |||
In each case, copy the pattern. Copy the + signs and copy the parentheses ( ). When you come to x, replace it with 10. When you come to y, replace it with 4. And when you come to z, replace it with 2.
Problem 5. Let x = 10, y = 4, z = 2, and evaluate the following.
| a) | x + 2(y + z) = | b) | (x + 2)(y + z) = | ||
| 10 + 2(4 + 2) = 10 + 2· 6 = 10 + 12 = 22. |
(10 + 2)(4 + 2) = 12· 6 = 72 | ||||
| c) | x − 3(y − z) = | d) | (x − 3)(y − z) = | ||
| 10 − 3(4 − 2) = 10 − 3· 2 = 10 − 6 = 4 |
(10 −3)(4 − 2) = 7· 2 = 14 | ||||
| e) | x − y + z = | f) | x − (y + z) = | ||
| 10 − 4 + 2 = 6 + 2 = 8 | 10 − (4 + 2) = 10 − 6 = 4 | ||||
g) x² − y² + 3z² = 100 − 16 + 3· 4 = 100 − 16 + 12 = 96
| h) | 10y² + 2z³ x² |
= | 10· 16 + 2· 8 100 |
| = | 160 + 16 100 |
||
| = | 176 100 |
||
| = | 1.76 | ||
Question 7. Why is a literal symbol also called a variable?
Because its value may vary.
A variable, such as x, is a kind of blank or empty symbol. It is therefore available to take any value we might give it: a positive number or, as we shall see, a negative number; a whole number or a fraction.
Problem 6. Two variables. Let the value of the variable y depend
on the value of the variable x as follows:
y = 2x + 4
Calculate the value of y that corresponds to each value of x:
When x = 0, y = 2· 0 + 4 = 0 + 4 = 4
When x = 1, y = 2· 1 + 4 = 2 + 4 = 6
When x = 2, y = 2· 2 + 4 = 4 + 4 = 8
When x = 3, y = 2· 3 + 4 = 6 + 4 = 10
When x = 4, y = 2· 4 + 4 = 8 + 4 = 12
Algebraic expressions
Problem 7. In algebra we often have to translate ordinary language into algebraic language. Write an algebraic expression that will symbolize each of the following.
a) Six times a certain number. 6n, or 6x, or 6m. Any letter will do.
b) Six more than a certain number. x + 6
c) Six less than a certain number. x − 6
d) A certain number subtracted from 6. 6 − x
e) A number repeated as a factor three times. x· x· x = x3
f) A number repeated as a term three times. x + x + x
g) The sum of three consecutive whole numbers. The idea, for example,
g) of 6 + 7 + 8. [Hint: Let x be the first number.]
g)
x + (x + 1) + (x + 2)
h) Eight less than twice a certain number. 2x − 8
i) One more than three times a certain number. 3x + 1
Now an algebraic expression is not a sentence; it does not have a verb, which is typically the equal sign = . An algebraic statement has an equal sign.
Problem 8. Write each statement algebraically.
a) The sum of two numbers is twenty. x + y = 20
b) The difference of two numbers is twenty. x − y = 20
c) The product of two numbers is twenty. xy = 20
d) Twice the product of two numbers is twenty. 2xy = 20
e) The quotient of two numbers is equal to the sum of those numbers.
| x y |
= x + y |
Formulas
A formula is an algebraic rule for evaluating some quantity. A formula is a statement.
Example. Here is the formula for the area A of a rectangle whose base is b and whose height is h.
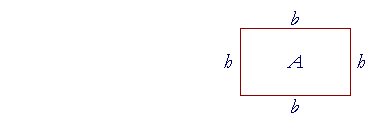
A = bh.
"The area of a rectangle is equal to the base times the height."
And here is the formula for its perimeter P -- that is, its boundary:
P = 2b + 2h.
"The perimeter of a rectangle is equal to two times the base
plus two times the height."
For, in a rectangle the opposite sides are equal.
Problem 9. Evaluate the formulas for A and P when b = 10 in, and h = 6 in.
A = bh = 10· 6 = 60 in²
P = 2b + 2h = 2· 10 + 2· 6 = 20 + 12 = 32 in
Problem 11. The area A of trapezoid is given by this formula,
A = ½(a + b)h.
Find A when a = 2 cm, b = 5 cm, and h = 4 cm.
A = ½(2 + 5)4 = ½· 7· 4 = 7· 2 = 14 cm²
Problem 12. The formula for changing temperature in degrees Fahrenheit (F) to degrees Celsius (C) is given by this formula:
| C = | 5 9 |
(F − 32) |
Find C if F = 68°.
| C = | 5 9 |
(68 − 32) = | 5 9 |
· 36 = 5· 4 = 20° |
www.proyectosalonhogar.com
