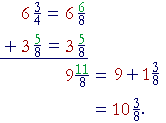| Example 1. |
5
8 |
+ |
2
8 |
= |
7
8 |
. |
Just as
5 apples + 2 apples = 7 apples,
so
5 eighths + 2 eighths = 7 eighths.
To add anything, the units -- the names -- must be the same. To add apples and oranges, you have to call them "piece of fruit"!
| In this problem, the unit is |
1
8 |
. We are adding eighths. (Lesson 20.) |
|
Example 2. |
5
8 |
− |
2
8 |
= |
3
8 |
. |
|
Solution. The lowest common multiple of 2 and 8, is 8 itself. We will
| change |
1
2 |
to a fraction whose denominator is 8. |
1
2 |
= |
4
8 |
, because 4 is half of 8. |
Therefore,
In practice, it is necessary to write the common denominator only once:
Solution. The LCM of 5 and
15 is 15. Therefore,
4
5 |
+ |
2
15 |
= |
12 + 2
15 |
= |
14
15 |
. |
4
5 |
has been changed to |
12
15 |
by multiplying both terms by 3. |
2
15 |
has not been changed |
, because we are keeping the denominator 15.
|
| Example 5. |
2
3 |
+ |
1
6 |
+ |
7
12 |
Solution. The LCM of 3, 6, and 12 is 12.
2
3 |
+ |
1
6 |
+ |
7
12 |
= |
8 + 2 + 7
12 |
2
3 |
+ |
1
6 |
+ |
7
12 |
= 1 |
5
12 |
. |
2
3 |
has been changed to |
8
12 |
by multiplying both terms by 4. |
1
6 |
has been changed to |
2
12 |
by multiplying both terms by 2. |
7
12 |
has not been changed, because we are keeping the denominator 12. |
| The improper fraction |
17
12 |
has been changed to 1 |
5
12 | by dividing 17 by 12. |
"12 goes into 17 one (1) time with remainder 5."
Solution. The LCM of 6 and 9 is 18.
5
6 |
+ |
7
9 |
= |
15 + 14
18 |
= |
29
18 |
= 1 |
11
18 |
. |
5
6 |
has been changed to |
15
18 |
by multiplying both terms by 3. |
7
9 |
has been changed to |
14
18 |
by multiplying both terms by 2. |
|
Example 7. Add mentally |
1
2 |
+ |
1
4 |
. |
| Answer. |
1
2 |
is how many |
1
4 |
's? |
1
2 |
= |
2
4 |
, because 2 is half of 4. |
Therefore,
The student should not have to write any problem in which one of
For example,
Example 8. In a recent exam, one eighth of the students got A, two fifths got B, and the rest got C. What fraction got C?
Solution. Let the whole number of students be represented by 1. Then the question is:
Now,
1
8 |
+ |
2
5 |
= |
5 + 16
40 |
= |
21
40 |
. |
| The rest, the fraction that got C, is the complement of |
21
40 |
. |
|
|
Example 9. 4 |
3
8 |
+ 2 |
2
8 |
= 6 |
5
8 |
. |
|
Example 10. 3 |
2
5 |
+ 1 |
4
5 |
= 4 |
6
5 |
. |
| But |
6
5 |
is improper, we must change it to a mixed number: |
Therefore,

Solution. When the denominators are different, we may arrange the work vertically.
To add the fractions, the denominators must be the same. The LCM
| of 4 and 8 is 8. We will change |
3
4 |
to |
6
8 |
-- we will multiply both terms |
by 2:
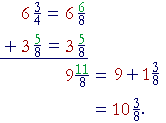
| We added 6 + 3 = 9. |
6
8 |
+ |
5
8 |
= |
11
8 |
= 1 |
3
8 |
. |
At this point, please "turn" the page and do some Problems.
or
Continue on to the next Section.
Introduction | Home | Table of Contents
www.proyectosalonhogar.com
|